Amp; 3.2. Поняття рівняння лінії на площині. Загальне рівняння прямої та його окремі випадки.
Рівняння 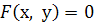 називається рівнянням деякої лінії L в заданій системі координат, якщо цьому рівнянню задовольняють координати
називається рівнянням деякої лінії L в заданій системі координат, якщо цьому рівнянню задовольняють координати 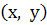 будь-якої точки, яка лежить на лінії L і не задовольняють координати ніякої точки, що не лежить на цій лінії.
будь-якої точки, яка лежить на лінії L і не задовольняють координати ніякої точки, що не лежить на цій лінії.
В прямокутній системі координат будь-яка пряма лінія задається рівнянням першого степеня відносно змінних х і у, тобто 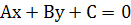 , яке називається загальним рівнянням прямої. Коефіцієнти А і В одночасно не дорівнюють нулю.
, яке називається загальним рівнянням прямої. Коефіцієнти А і В одночасно не дорівнюють нулю.
Розглянемо окремі випадки загального рівняння прямої.
1. Якщо С = 0, то рівняння має вигляд 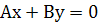 . Пряма проходить через початок координат.
. Пряма проходить через початок координат.
2. Якщо А = 0. Маємо рівняння прямої 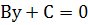 . (у = b), яка паралельна осі ОХ.
. (у = b), яка паралельна осі ОХ.
3. Якщо В = 0. Рівняння прямої має вигляд 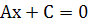 (х = a). Пряма паралельна осі ОУ.
(х = a). Пряма паралельна осі ОУ.
4. Якщо А = С = 0, то у = 0. Пряма збігається з віссю ОХ.
5. Якщо В = С = 0, то х = 0. Пряма збігається з віссю ОУ.
Приклад 1. Побудувати прямі : 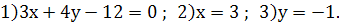
Розв’язання.
1) Щоб побудувати пряму 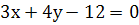 , знаходимо координати точок перетину з осями ОХ і ОУ. Припустивши, що у = 0, дістанемо
, знаходимо координати точок перетину з осями ОХ і ОУ. Припустивши, що у = 0, дістанемо 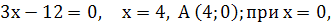 дістанемо
дістанемо 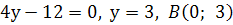 . Через точки А і В проводимо шукану пряму :
. Через точки А і В проводимо шукану пряму :
| у |
| х |
| А(4; 0) |
| В(0; 3) |
| у |
| х |
| А(4; 0) |
| В(0; 3) |
2)
| х |
| у |
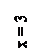 На осі ОХ візьмемо точку х = 3 і проведемо пряму, паралельну осі ОУ.
На осі ОХ візьмемо точку х = 3 і проведемо пряму, паралельну осі ОУ.
3)
| у = -1 |
| х |
| у |
| -1 |
Дата добавления: 2015-06-27; просмотров: 5396;
