Властивості векторного добутку.
1. Векторний добуток 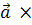
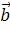 дорівнює нулю, якщо вектори
дорівнює нулю, якщо вектори 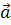 і
і 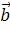 колінеарні, або один з них – нульовий.
колінеарні, або один з них – нульовий.
2. 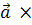
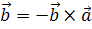 .
.
3. 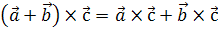 .
.
4. 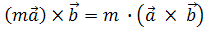 .
.
Векторний добуток векторів 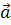 (х1; у1;
(х1; у1; 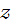 1) і
1) і 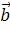 (х2; у2;
(х2; у2; 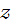 2), заданих своїми координатами, обчислюється так :
2), заданих своїми координатами, обчислюється так :
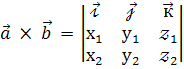
Приклад 6. Знайдіть площу паралелограма, побудованого на векторах 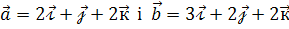 .
.
Розв’язання.
Модуль векторного добутку, двох векторів дорівнює площі паралелограма, побудованого на цих векторах. Знаходимо векторний добуток :
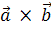
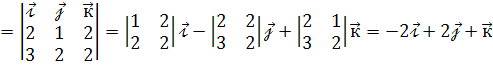 .
.
Знаходимо модуль векторного добутку :
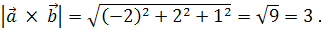
Шукана площа S = 3 (кВ. од.).
& 2.7. Мішаний добуток векторів. Умова компланарності векторів.
Означення. Мішаним добутком трьох векторів 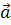 ,
, 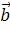 ,
,  називається число, яке дорівнює скалярному добутку вектора
називається число, яке дорівнює скалярному добутку вектора 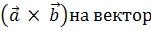
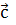
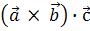 ,
,
де вектори 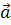 ,
, 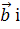
 некомпланарні .
некомпланарні .
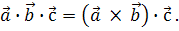
Модуль мішаного добутку дорівнює об’єму паралелепіпеда, побудованого на векторах 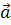 ,
, 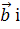
 .
.
Умова компланарності векторів.
Якщо вектори 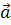 ,
, 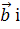
 компланарні, то мішаний добуток їх дорівнює нулю :
компланарні, то мішаний добуток їх дорівнює нулю :
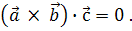
Мішаний добуток векторів, заданих своїми координатами, 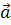 (х1; у1;
(х1; у1; 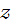 1) і
1) і 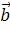 (х2; у2;
(х2; у2; 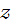 2),
2),  (х3; у3;
(х3; у3; 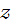 3) обчислюється за формулою :
3) обчислюється за формулою :
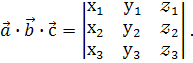
Приклад 7. Знайдіть об’єм паралелепіпеда, побудованого на векторах , 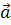 (4; -1; 1) ,
(4; -1; 1) , 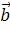 (8; 3; 3),
(8; 3; 3),  (5; 1; 1).
(5; 1; 1).
Розв’язання.
Знайдемо мішаний добуток трьох векторів :
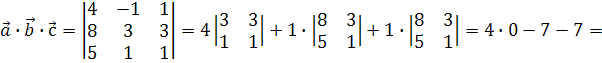
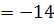
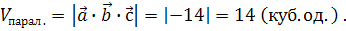
Питання для самоконтролю.
1. Дати визначення вектора.
2. Як обчислюються координати вектора через координати його початку і кінця?
3. Які дії над векторами, заданими координатами, можна виконувати?
4. Яка умова колінеарності двох векторів?
5. Як обчислюється довжина вектора через координати?
6. Дати означення скалярного добутку векторів.
7. Яка формула скалярного добутку векторів в координатній формі?
8. За якою формулою знаходиться кут між векторами?
9. Дати означення векторного добутку двох векторів.
10. Яка формула векторного добутку векторів в координатній формі?
11. Дати означення мішаного добутку трьох векторів.
12. Яка формула мішаного добутку векторів в координатній формі?
13. Яка умова компланарності векторів?
Дата добавления: 2015-06-27; просмотров: 6332;
