В случае векторного способа задания движения вектор скорости точки равен первой производной по времени от ее радиус-вектора

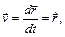(1.4)

где точка над функцией в теоретической механике означает первую производную по времени, а две точки – вторую производную по времени. Производные по другим переменным записывают обычным образом. Вектор скорости точки приложен в самой точке и направлен по касательной к траектории в сторону движения точки. Единица измерения скорости в системе СИ – 1 м/с.

При координатном способе задания движения точки ее скорость определяют через проекции вектора скорости на оси выбранной системы координат, которые равны первым производным от соответствующих координат по времени:

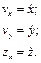(1.5)

Если известны проекции скорости на оси координат, то модуль вектора скорости и его направляющие косинусы находят по формулам:

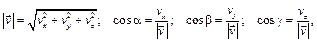(1.6)

где 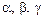– углы между вектором скорости и осями координат. При естественном способе задания движения точки вектор ее скорости определяют по формуле

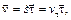(1.7)

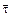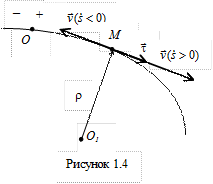
где – единичный вектор касательной к траектории в данной точке, направленный всегда в сторону положительного отсчета криволинейной координаты S. Скалярную величину 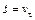, являющуюся проекцией вектора скорости на касательную к траектории, называют алгебраической скоростью точки (рис. 1.4). Знак алгебраической скорости определяет направление движения точки: если 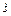> 0, то вектор скорости совпадает по направлению с вектором 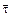; в противном случае он направлен в противоположную сторону. На рисунке точка О₁ означает центр кривизны траектории, а 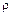– радиус кривизны в точке М.