Ускорение точки

Ускорение точки является векторной мерой изменения ее скорости, как по величине, так и по направлению. При векторном способе задания движения вектор ускорения точки равен первой производной по времени от вектора ее скорости или второй производной по времени от ее радиус-вектора:

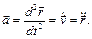(1.8)

Вектор ускорения приложен к движущейся точке, лежит в соприкасающейся плоскости к траектории в данной точке и направлен в общем случае в сторону вогнутости траектории. Единица измерения ускорения в системе СИ – 1 .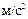

При координатном способе задания движения точки вектор ускорения определяют через его проекции на оси координат, которые равны вторым производным от соответствующих координат по времени:

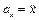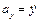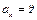, , . (1.9)

Если известны проекции ускорения на оси координат, то модуль вектора ускорения и его направляющие косинусы находят по формулам:

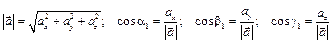, (1.10)

где 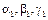– углы между вектором ускорения и осями координат.

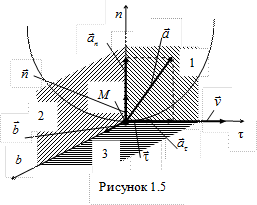При естественном способе задания движения с движущейся точкой связывают естественную систему координат (рис. 1.5). Естественный трехгранник составляется из трех пересекающихся взаимно перпендикулярных плоскостей: 1 – соприкасающейся, 2 – нормальной и

3 – спрямляющей. Линии пересечения плоскостей образуют правую систему естественных осей координат: τ, n и b, определяемых единичными векторами 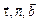, которые называют единичными векторами касательной, главной нормали и бинормали соответственно.

Вектор ускорения точки в естественной системе определяют по формулам:

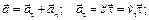
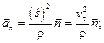(1.11)

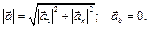
Здесь 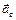– касательное или тангенциальноеускорение точки, которое направлено по касательной к траектории в сторону движения, если движение ускоренное (алгебраическая скорость точки возрастает), и в противоположную сторону, если движение замедленное (алгебраическая скорость точки убывает). Нормальноеускорение 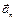всегда направлено по нормали к траектории в сторону вогнутости. Поскольку вектор ускорения точки лежит в соприкасающейся плоскости, то его проекция на бинормаль 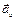равна нулю. Касательное ускорение характеризует изменения скорости точки по модулю, а нормальное – по направлению.

Касательное ускорение точки по величине и направлению можно определить по известным проекциям векторов скорости и ускорения на координатные оси по формуле

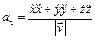. (1.12)