Nbsp; Разность расстояний от источников до рассматриваемой точки называется разностью хода волн
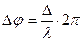Разность хода дает разность фаз, которую несложно рассчитать через длину волны (пока мы рассматривает случай, когда волны распространяются в одной среде):
В общем случае разность фаз волн, приходящих в какую-либо точку среды, равна
.
Все становится намного проще, если источники волн колеблются в одной фазе. Тогда разность фаз волн обусловлена только их разностью хода. В этом случае условия максимума и минимума можно сформулировать иначе.
Для точек максимума на разности хода должно укладываться целое число длин волн:
 |
 |
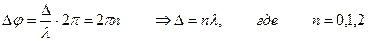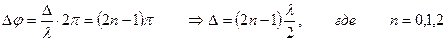Для точек минимума на разности хода должно укладываться нечетное число полуволн:
Стоячие волны
Частным случаем интерференции является наложение падающей и отраженной волны, бегущей в противоположном направлении. Такое явление наблюдается, если дернуть за струну музыкального инструмента. По ней побежит волна, она отразится от точки закрепления струны, и мы будем наблюдать результат наложения падающей и отраженной волн.
Очень важный случай интерференции наблюдается при наложении встречных волн одной амплитуды. Исследуем эффект теоретически.
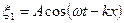Уравнение бегущей волны
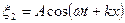Уравнение встречной волны
Результирующее колебание
 |
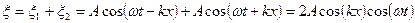
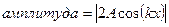Нетрудно видеть, что в результате наложения двух встречных волн все точки колеблются с той же частотой w, что и встречные волны. Но вот амплитуды разных точек на оси ОХ, вдоль которой распространялись волны, разные.
В точках, координаты которых удовлетворяют условию
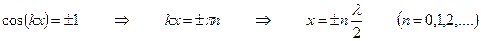
амплитуда колебаний достигает максимального значения 2А. Эти точки называются пучностями стоячей волны.
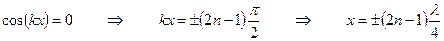
В точках, координаты которых удовлетворяют условию
Амплитуда колебаний обращается в ноль. Эти точки называются узлами стоячей волны. Точки, находящиеся в узлах стоячей волны, колебаний не совершают!!!
Расстояние между соседними узлами, как и между соседними пучностями, равно l/2. Пучности и узлы сдвинуты относительно друг друга на четверть длины волны.
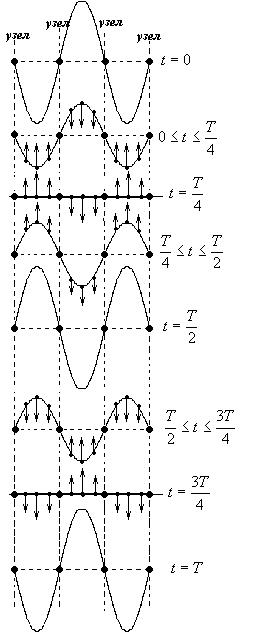
На рисунке показан ряд моментальных «фотографий» отклонения точек от положения равновесия в стоячей волне. Стрелками показаны скорости частиц.
Все точки, расположенные между двумя соседними узлами, колеблются в одной фазе: они одновременно проходят положение равновесия и одновременно приходят в положение максимального отклонения от положения равновесия.
Видно, что точки по разные стороны от узлов колеблются в противофазе.
Почему стоячие волны столь важны в физике?
Вернемся к струне, закрепленной с двух сторон. При возбуждении колебаний в ней устанавливается стоячая волна. Причем в местах закрепления у этой волны должны располагаться узлы, ибо эти точки колебаться не могут. Поэтому в струне возбуждаются с заметной амплитудой только такие колебания, половина длины которых укладывается на длине струны целое число раз. Например, закрепленная струна может совершать следующие колебания:
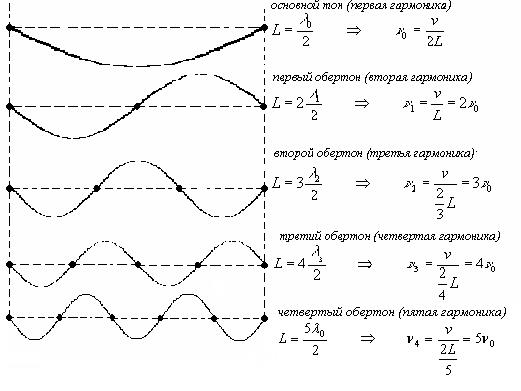и т.д.
Частоты n0, n1, n2, n3 и т.д. называются для струны собственными частотами (или нормальными колебаниями). В общем случае колебания струны представляет собой наложение различных гармоник, т.е. струна одновременно участвует в нескольких собственных колебаниях.
Наибольшая амплитуда колебаний , как правило, будет на частоте основного тона. Чем выше номер гармоники, тем амплитуда колебаний будет меньше. Поэтому основной тон мы и слышим громче всего.
Дата добавления: 2015-06-12; просмотров: 2081;