Принцип Гюйгенса – Френеля

В 1690 году Гюйгенс сформулировал принцип, позволивший объяснить процесс распространения волн и из свойства – отражение, преломление и дифракцию.

Суть принципа заключается в следующем: каждая точка среды, до которой дошел волновой процесс, становится источником вторичных сферических волн. Чтобы построить волновой фронт, нужно провести огибающую этих вторичных сферических волн.

Физическое толкование принципа Гюйгенса было дано Френелем: вторичные сферические волны когерентны, они интерферируют. В направлении распространения волны вторичные сферические волны, интерферируя, усиливают друг друга, в противоположном направлении – гасят.

Применим принцип Гюйгенса – Френеля к объяснению явлений отражения и преломления.

Отражением называют явление возвращения волны в первоначальную среду при попадании на границу раздела двух сред.

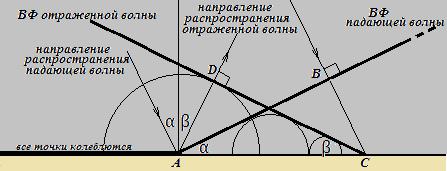
Пусть на границу раздела двух сред падает плоская волна.

Углом падения называют угол между направлением распространения волны и перпендикуляром к границе раздела двух сред, восстановленным из точки падения (на рис. угол α) .

Видно, что волна дошла до всех точек границы, расположенных левее точки А. Эти точки колеблются, от них бегут вторичные сферические волны.

За то время t, что падающая волна дойдет от точки В до точки С, расположенной на границе раздела, все точки отрезка АС будут вовлечены в колебательный процесс, от них побегут вторичные сферические волны. Волновой фронт отраженной волны строится как огибающая этих вторичных сферических волн.

Направление распространения отраженной волны перпендикулярно фронту отраженной волны. Угол между направлением распространения отраженной волны и перпендикуляром к границе раздела двух сред, восстановленным из точки падения, называется углом отражения (на рис. угол β).

Рассмотрим прямоугольные треугольники ABC и ADC.

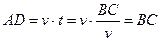Сторона АС в этих треугольниках общая. Расстояние АD – это путь, пройденный вторичной волной за то время, пока падающая волна идет от В до С:

где v – скорость распространения волны.

Таким образом, ∆ABC = ∆ADC. В равных треугольниках против равных сторон ( 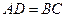) находятся одинаковые углы α = β. Угол падения равен углу отражения.

Преломлениемназывается изменение направления распространения волны при переходе из одной среды в другую.

Пусть плоская волна переходит из среды, где скорость ее распространения равна 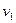, в среду, где скорость распространения волны .

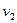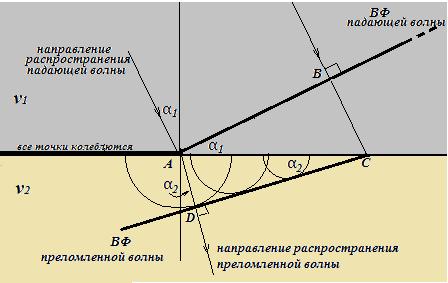
За то время t, что падающая волна дойдет от точки В до точки С, расположенной на границе раздела, все точки отрезка АС будут вовлечены в колебательный процесс, от них побегут вторичные сферические волны во вторую среду. Волновой фронт отраженной волны строится как огибающая этих вторичных сферических волн.

Направление распространения прошедшей во вторую среду волны перпендикулярно фронту отраженной волны. Угол между направлением распространения прошедшей волны и перпендикуляром к границе раздела двух сред, восстановленным из точки падения, называется углом преломления(на рис. угол α₂).

В прямоугольных треугольниках ABC и ADC

Находим отношение синусов углов падения и преломления

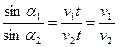
Полученный результат свидетельствует о том, что причиной изменения направления распространения волны при переходе из одной среды в другую является изменение скорости волны.

Дифракция – явление огибания волнами преград и попадания в область геометрической тени.

Например, вы слышите музыку, находясь по обратную сторону летней эстрады. Стоя за глухим высоким забором школьного стадиона, вы слышите крики болельщиков. Круговая волна на поверхности воды, проходя через зазор в преграде, распространяется не параллельным пучком, а расходится, попадает в области за преградой.

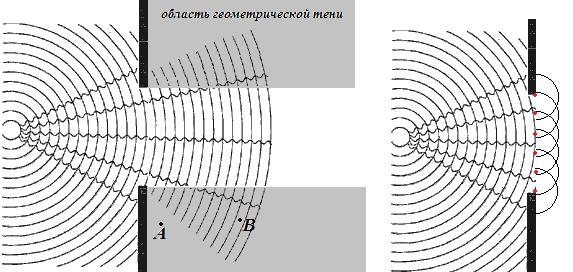
Качественное объяснение явлению можно дать, опять-таки используя принцип Гюйгенса – Френеля. От каждой точки отверстия распространяется вторичная сферическая волна. Оказывается, что в области геометрической тени вторичные сферические волны, интерферирую, не гасят друг друга. Таким образом, волна огибает преграду, попадает за преграду. Степень расхождения волны после прохождения отверстия (преграды) зависит от размеров отверстия, длины волны и удаленности наблюдателя от отверстия (в точке А на рисунке волны нет, а в точку В волна пришла). Чем меньше отверстие (преграда), тем степень расхождения (схождения) волны за ней будет больше.