II.ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. 3 страница
Размерность кинетического момента в СИ—кг·м2/с, или Н·м·с.
Определение. Кинетическим моментом или главным моментом количества движения 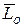 механической системы относительно полюса называется вектор, равный геометрической сумме кинетических моментов всех материальных точек системы относительно этого полюса:
механической системы относительно полюса называется вектор, равный геометрической сумме кинетических моментов всех материальных точек системы относительно этого полюса:
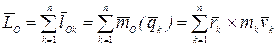 .
.
Определение. Кинетическим моментом или главным моментом количества движения механической системы 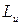 относительно оси называется алгебраическая сумма кинетических моментов всех материальных точек системы относительно этой оси:
относительно оси называется алгебраическая сумма кинетических моментов всех материальных точек системы относительно этой оси:
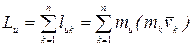 .
.
Кинетические моменты механической системы относительно полюса и оси, проходящей через этот полюс, связаны такой же зависимостью, как и главные моменты системы сил относительно полюса и оси:
—проекция кинетического момента механической системы относительно полюса 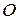 на ось
на ось 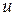 , проходящую через этот полюс, равна кинетическому моменту системы относительно этой оси, т. е.
, проходящую через этот полюс, равна кинетическому моменту системы относительно этой оси, т. е.
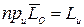 .
.
4.3.2. Теоремы об изменении кинетического момента механической системы.
Рассмотрим механическую систему, состоящую из 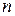 материальных точек, массы которых
материальных точек, массы которых 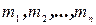 . Докажем теорему об изменении кинетического момента механической системы относительно полюса.
. Докажем теорему об изменении кинетического момента механической системы относительно полюса.
Теорема. Производная по времени от кинетического момента механической системы относительно неподвижного полюса равна главному моменту внешних сил системы относительно того же полюса, т. е.
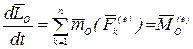 .
.
Теорема. Производная по времени от кинетического момента механической системы относительно неподвижной оси равна главному моменту внешних сил системы относительно той же оси, т. е.
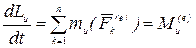 .
.
4.3.3. Законы сохранения кинетического момента
(следствия из теоремы)
Следствие 1. Если главный момент внешних сил системы относительно неподвижного полюса равен нулю, то кинетический момент этой системы относительно того же полюса будет постоянным как по величине, так и по направлению.
Действительно, на основании (4.22) имеем: 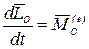 . Если
. Если 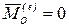 , то
, то 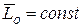 .
.
Следствие 2. Если главный момент внешних сил системы относительно неподвижной оси равен нулю, то кинетический момент этой системы относительно той же оси будет постоянным.
Если 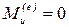 , тогда по формуле (4.27):
, тогда по формуле (4.27): 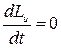 и
и 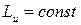 .
.
4.3.4. Кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения.
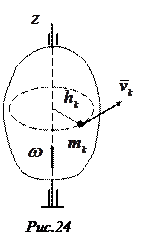 Рассмотрим твердое тело, вращающееся вокруг неподвижной оси
Рассмотрим твердое тело, вращающееся вокруг неподвижной оси 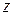 с угловой скоростью
с угловой скоростью 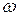 (рис.24). Кинетический момент материальной точки
(рис.24). Кинетический момент материальной точки
массы 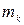 относительно оси
относительно оси 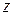 (формула (4.18)):
(формула (4.18)):
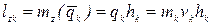 .
.
Учитывая, что 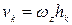 , где
, где 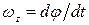 —алгебраическая угловая скорость тела:
—алгебраическая угловая скорость тела:
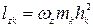 .
.
Кинетический момент тела относительно оси будет, согласно (4.20), равен алгебраической сумме этих выражений для всех точек тела
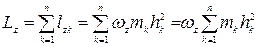
Определение. Моментом инерции твердого тела (механической системы) относительно оси называется сумма произведений масс всех точек тела (системы) на квадрат их расстояний от этой оси, т. е.
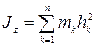
Размерность момента инерции в системе СИ—кг·м2. Часто при вычислениях применяют понятие радиуса инерции. Радиусом инерции тела относительно оси называется величина 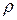 , определяемая равенством
, определяемая равенством
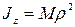 ,
,
где 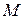 —масса тела.
—масса тела.
Возвращаясь к формуле (4.32), получаем
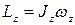 ,
,
т. е. кинетический момент твердого тела, вращающегося вокруг неподвижной оси, относительно оси вращения равен произведению момента инерции тела относительно оси вращения на алгебраическую угловую скорость этого тела.
Теорема.Момент инерции механической системы относительно некоторой оси 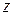 равен моменту инерции относительно параллельной оси
равен моменту инерции относительно параллельной оси 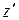 , проходящей через центр масс системы, сложенному с произведением массы
, проходящей через центр масс системы, сложенному с произведением массы 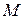 системы на квадрат расстояния
системы на квадрат расстояния 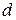 между осями, т. е.
между осями, т. е.
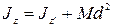 . (4.41)
. (4.41)
1. Тонкий однородный стержень длиной 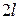 и массой
и массой 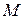 . Вычислим его момент инерции относительно симметрии
. Вычислим его момент инерции относительно симметрии 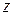 (рис. 28).
(рис. 28).
Направим вдоль оси стержня координатную ось 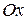 . Для любого элементарного отрезка длины
. Для любого элементарного отрезка длины 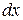 величина
величина 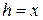 , масса
, масса 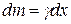 , где
, где 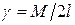 —масса единицы длины стержня (линейная плотность). В соответствии с формулой (4.42)
—масса единицы длины стержня (линейная плотность). В соответствии с формулой (4.42)
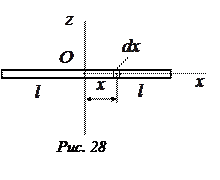
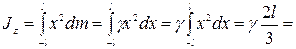
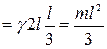 .
.
Окончательно
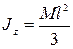 .
.
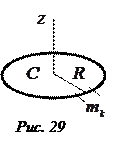 2. Тонкое круглое однородное кольцо радиуса
2. Тонкое круглое однородное кольцо радиуса 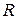 и массы
и массы 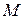 . Вычислим момент инерции относительно оси
. Вычислим момент инерции относительно оси 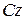 , перпендикулярной плоскости кольца и проходящей через его центр
, перпендикулярной плоскости кольца и проходящей через его центр 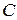 (рис.29).
(рис.29).
Так как все точки кольца находятся от оси 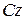 на расстоянии
на расстоянии 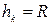 , то по формуле (4.33):
, то по формуле (4.33):
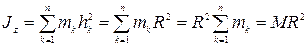 .
.
Окончательно
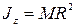 .
.
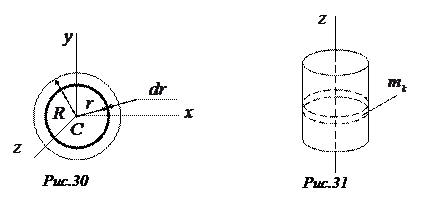 |
3. Круглая однородная пластина или цилиндр радиуса
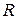 и массой
и массой 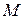 .
.
Вычислим момент инерции круглой однородной пластины относительно оси 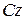 , перпендикулярной пластине и проходящей через ее центр (рис.30). Для этого выделим элементарное кольцо радиусом
, перпендикулярной пластине и проходящей через ее центр (рис.30). Для этого выделим элементарное кольцо радиусом 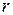 и шириной
и шириной 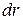 . Площадь этого кольца
. Площадь этого кольца 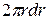 , а масса
, а масса 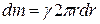 , где
, где 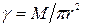 —масса единицы площади пластины. Тогда по формуле (4.44) для выделенного элементарного кольца
—масса единицы площади пластины. Тогда по формуле (4.44) для выделенного элементарного кольца
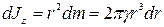 ,
,
а для всей пластины
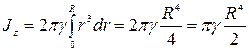 .
.
Заменяя 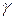 его значением, получим окончательно
его значением, получим окончательно
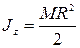 .
.
Такая же формула получится и для момента инерции 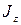 однородного круглого цилиндра массой
однородного круглого цилиндра массой 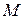 и радиусом
и радиусом 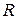 относительно его оси (рис.31). Для доказательства этого разобьем цилиндр на элементарные пластины массой
относительно его оси (рис.31). Для доказательства этого разобьем цилиндр на элементарные пластины массой 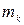 . Момент инерции каждой из этих пластин относительно оси
. Момент инерции каждой из этих пластин относительно оси 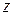 определяется формулой (4.45):
определяется формулой (4.45):
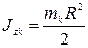 .
.
Момент инерции цилиндра относительно оси 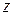 равен сумме моментов инерции всех элементарных пластин относительно той же оси, т. е.
равен сумме моментов инерции всех элементарных пластин относительно той же оси, т. е.
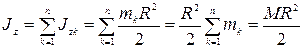 .
.
4.4. Теорема об изменении кинетической энергии.
4.4.1. Работа постоянной силы.
Рассмотрим сначала вычисление работы силы в весьма частном случае. Пусть на материальную точку 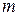 действует сила
действует сила 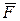 , постоянная по величине и направлению, и эта точка приложения силы перемещается прямолинейно из положения
, постоянная по величине и направлению, и эта точка приложения силы перемещается прямолинейно из положения 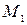 в положение
в положение 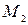 (рис. 35).
(рис. 35).
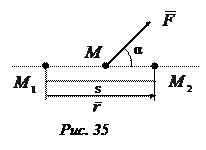 В рассматриваемом случае работой силы
В рассматриваемом случае работой силы 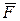 называется произведение модуля силы на перемещение
называется произведение модуля силы на перемещение 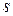 её точки приложения и на косинус угла между направлением вектора силы и направлением перемещения точки приложения силы, т. е.
её точки приложения и на косинус угла между направлением вектора силы и направлением перемещения точки приложения силы, т. е.
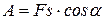 .
.
Если угол 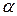 острый, то работа силы
острый, то работа силы 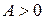 , а если тупой, то
, а если тупой, то 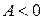 .
.
Если направления вектора силы и перемещения её точки приложения совпадают, т. е. 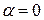 , то
, то 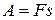 .
.
Если направление вектора силы перпендикулярно перемещению её точки приложения, т. е. 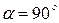 , то
, то 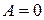 .
.
Если направление вектора силы противоположно направлению перемещения её точки приложения, то 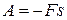
4.4.2. Элементарная работа силы.
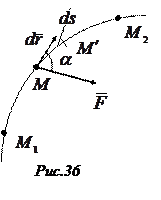 Пусть сила переменна как по величине, так и по направлению, а её точка
Пусть сила переменна как по величине, так и по направлению, а её точка
приложения (материальная точка 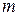 ) перемещается по криволинейной траектории (рис.36).
) перемещается по криволинейной траектории (рис.36).
Вычислим работу силы 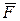 на элементарном участке
на элементарном участке 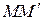 —элементарном перемещении точки приложения силы
—элементарном перемещении точки приложения силы 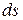 . Этот участок можно считать прямолинейным, тогда вектор элементарного перемещения
. Этот участок можно считать прямолинейным, тогда вектор элементарного перемещения 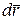 точки
точки 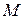 , направлен по касательной к траектории в сторону движения точки и по величине . Кроме того, можно считать, что сила на рассматриваем элементарном участке постоянна по величине и направлению.
, направлен по касательной к траектории в сторону движения точки и по величине . Кроме того, можно считать, что сила на рассматриваем элементарном участке постоянна по величине и направлению.
Определение. Элементарной работой силы 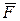 называется произведение модуля силы
называется произведение модуля силы 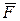 на элементарное перемещение её точки приложения и на косинус угла между вектором силы и вектором элементарного перемещения
на элементарное перемещение её точки приложения и на косинус угла между вектором силы и вектором элементарного перемещения 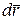 , т. е.
, т. е.
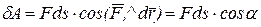 .
.
Элементарную работу можно также записать в виде
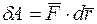
Элементарную работу обозначают 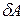 , а не
, а не 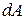 , так как в общем случае она не является дифференциалом функции.
, так как в общем случае она не является дифференциалом функции.
Если силу 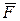 и вектор элементарного перемещения
и вектор элементарного перемещения 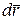 разложить по осям
разложить по осям
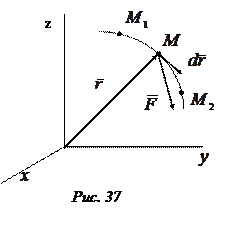 координат (рис.37), то
координат (рис.37), то
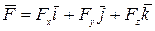 ,
, 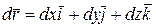 .
.
Подставляя в (4.59) значения 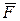 и
и 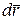 ,получаем формулу для элементарной работы в проекциях на оси координат
,получаем формулу для элементарной работы в проекциях на оси координат
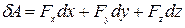 .
.
Элементарная работа силы 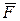 равна сумме произведения проекций этой силы на оси координат на дифференциалы соответствующих координат точки приложения силы.
равна сумме произведения проекций этой силы на оси координат на дифференциалы соответствующих координат точки приложения силы.
4.4.3. Работа силы на конечном перемещении.
Определим работу силы 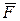 на конечном перемещении её точки приложения
на конечном перемещении её точки приложения 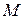 из положения
из положения 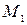 в положение
в положение 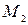 .Для этого разобьем это перемещение на
.Для этого разобьем это перемещение на 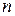 перемещений, каждое из которых в пределе—элементарное. Тогда работа может быть выражена как
перемещений, каждое из которых в пределе—элементарное. Тогда работа может быть выражена как
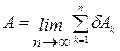 ,
,
где 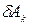 —работа силы
—работа силы 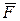 на
на 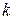 -ом элементарном перемещении, на которые разбито полное перемещение. Так как сумма в этом выражении для работы является интегральной суммой, то работа силы
-ом элементарном перемещении, на которые разбито полное перемещение. Так как сумма в этом выражении для работы является интегральной суммой, то работа силы 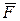 на конечном перемещении её точки приложения выражается криволинейным интегралом:
на конечном перемещении её точки приложения выражается криволинейным интегралом:
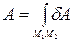 =
= 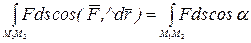 .
.
Теорема (о работе равнодействующей). Работа равнодействующей системы сил на каком либо перемещении равна алгебраической сумме работ составляющих сил на том же перемещении.
Теорема(о работе силы на последовательных перемещениях).Работа силы на конечном перемещении равна сумме работ этой же силы на последовательных составляющих перемещениях, на которые любым образом разбито исходное конечное перемещение.
Доказательство следует из возможности разбиения любым образом всего промежутка интегрирования на составляющие, причем интеграл по всему промежутку интегрирования равен сумме интегралов по составляющим.
Наряду с понятием работы вводят также понятие мощности.
Мощностью силы называется отношение элементарной работы к элементарному промежутку времени, за который она совершена
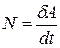 .
.
Если учесть, что 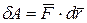 , то
, то
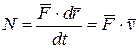 ,
,
т. е. мощность равна скалярному произведению силы на скорость.
За единицу работы в СИ принимают джоуль: 1 Дж=1 Н·м, за единицу мощности ватт: 1 Вт=1 Дж/с.
4.4.4. Работа силы тяжести.
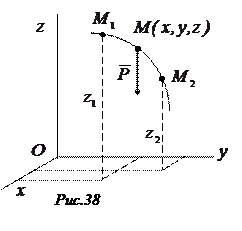 Пусть точка
Пусть точка 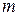 , на которую действует сила тяжести
, на которую действует сила тяжести 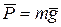 , переместилась из положения
, переместилась из положения 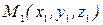 в положение
в положение 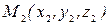 (рис.38).
(рис.38).
Вычислим работу силы 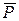 . Вблизи поверхности Земли силу тяжести можно считать постоянной и направленной по вертикали вниз. Ее проекции на оси координат
. Вблизи поверхности Земли силу тяжести можно считать постоянной и направленной по вертикали вниз. Ее проекции на оси координат
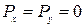 ,
, 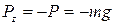 . Элементарная работа—формула (4.61):
. Элементарная работа—формула (4.61):
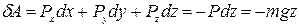 Работа силы
Работа силы 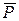 на перемещении
на перемещении 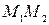 :
:
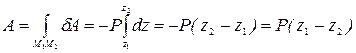
Окончательно
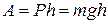 ,
,
где 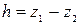 — падение высоты.
— падение высоты.
Работа силы тяжести равна произведению силы тяжести на падение высоты ее точки приложения. Если точка приложения силы тяжести опускается 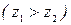 , то работа положительная, если поднимается
, то работа положительная, если поднимается 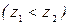 —отрицательная.
—отрицательная.
Работа силы тяжести не зависит от формы траектории ее точки приложения, а зависит только от начального и конечного положений этой точки приложения.
4.4.5. Работа силы упругости.
Пусть на материальную точку 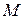 действует упругая сила
действует упругая сила 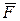 —реакция пружины. Выберем начало координат в положении, при котором пружина не напряжена (рис. 39). По закону Гука
—реакция пружины. Выберем начало координат в положении, при котором пружина не напряжена (рис. 39). По закону Гука 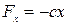 , где
, где 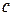 —коэффициент жесткости пружины. Вычислим работу силы упругости
—коэффициент жесткости пружины. Вычислим работу силы упругости 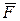 на перемещении её точки приложения
на перемещении её точки приложения 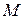 из положения
из положения 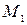 в положение
в положение 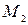 . Проекции силы
. Проекции силы 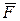 на оси координат:
на оси координат:
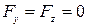 ,
, 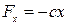 ;
;
её элементарная работа:
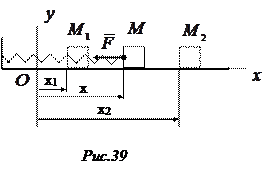
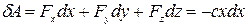
полная работа
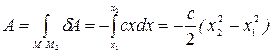
Окончательно
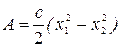 .
.
При выбранном начале координат координаты 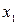 и
и 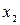 представляют собой начальную и конечную деформации (удлинение или укорочение) пружины, т. е.
представляют собой начальную и конечную деформации (удлинение или укорочение) пружины, т. е. 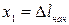 ,
, 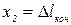 . Поэтому
. Поэтому
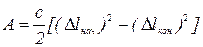 .
.
4.4.6. Работа сил, приложенных к твердому телу.
1. Работа внутренних сил.
Твердое тело—это механическая система, расстояния между точками которой, остаются постоянными. Пусть между точками 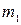 и
и 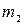 действуют внутренние силы взаимодействия:
действуют внутренние силы взаимодействия: 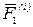 —сила, действующая на точку
—сила, действующая на точку 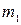 со стороны точки
со стороны точки 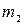 ,
, 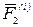 —сила, действующая на точку
—сила, действующая на точку 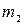 со стороны точки
со стороны точки 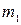 (рис. 40). По третьему закону Ньютона
(рис. 40). По третьему закону Ньютона 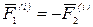 . Составим сумму мощностей сил
. Составим сумму мощностей сил 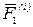 и
и 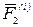
(формула (4.67)):
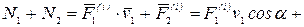
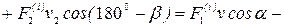
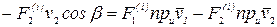 .
.
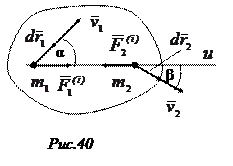 В кинематике твердого тела было установлено, что проекции скоростей любых двух точек твердого тела на направление прямой линии, соединяющей эти точки, алгебраически равны при произвольном движении тела, т. е.
В кинематике твердого тела было установлено, что проекции скоростей любых двух точек твердого тела на направление прямой линии, соединяющей эти точки, алгебраически равны при произвольном движении тела, т. е.
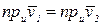 , кроме того
, кроме того 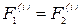 , поэтому
, поэтому
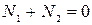 .
.
Получили, что сумма мощностей сил 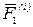 и
и 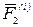 равна нулю, а, следовательно, и сумма работ сил
равна нулю, а, следовательно, и сумма работ сил 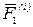 и
и 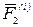 равна нулю. Твердое тело можно считать состоящим из пар взаимодействующих точек, для каждой из которых сумма работ внутренних сил равна нулю. Суммируя работы для всех пар точек, получаем, что работа внутренних сил абсолютно твердого тела равна нулю.
равна нулю. Твердое тело можно считать состоящим из пар взаимодействующих точек, для каждой из которых сумма работ внутренних сил равна нулю. Суммируя работы для всех пар точек, получаем, что работа внутренних сил абсолютно твердого тела равна нулю.
2. Поступательное движение твердого тела.
Вычислим работу внешних сил, приложенных к твердому телу, совершающему поступательное движение. Пусть 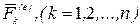 —равнодействующая внешних сил, действующих на точку
—равнодействующая внешних сил, действующих на точку 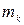 (рис.41). Элементарная работа силы
(рис.41). Элементарная работа силы 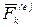 :
:
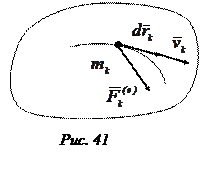
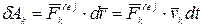
При поступательном движении твердого тела скорости всех его точек геометрически равны между собой
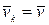 ,
, 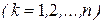 .
.
Тогда элементарная работа всех сил, приложенных к твердому телу, рана элементарной работе внешних сил
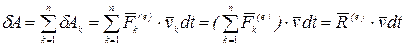 ,
,
где 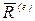 —главный вектор внешних сил. Следовательно,
—главный вектор внешних сил. Следовательно,
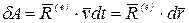 ,
,
т. е. элементарная работа сил, приложенных к твердому телу, совершающему поступательное движение, равна элементарной работе главного вектора внешних сил, приложенного в любой точке тела.
Работа на конечном перемещении
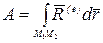 .
.
3. Работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси.
Сила 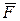 приложена к точке
приложена к точке 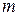 твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью
твердого тела, вращающегося вокруг неподвижной оси с угловой скоростью 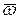 (рис. 42). Вычислим элементарную работу этой силы:
(рис. 42). Вычислим элементарную работу этой силы:
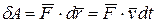 .
.
По полученной в кинематике первой формуле Эйлера
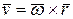 ,
,
где 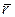 —радиус-вектор точки
—радиус-вектор точки 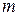 относительно произвольного полюса
относительно произвольного полюса 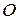 , лежащего на оси вращения. Тогда
, лежащего на оси вращения. Тогда
Дата добавления: 2015-04-21; просмотров: 2179;
