1 страница. Основы классификации механизмов
Основы классификации механизмов. Основные понятия и определения.
Курс изучает общие свойства, характеристик для механизмов и машин, методы исследования и проектирования на схемном уровне. При этом имеют место две основные задачи: задачи синтеза и задачи анализа машин
Это можно представить так: 
Говоря о машине как таковой, мы представляем её в виде структурной схемы, т.е. изображение без масштаба, отражающую лишь структуру механизма. Если схема дается в масштабе то имеет место кинематическая схема (она позволяет определить кинематические параметры машины)
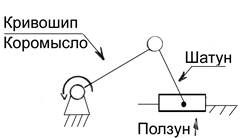
Дадим определение термина “Машина”, и введем основные понятия:
Машина состоит: из одного или нескольких машинных агрегатов
 Машинный агрегат:
Машинный агрегат:
Механизмом называется система тел, предназначенная для преобразования движения одного или нескольких тел в требуемые движения других тел. Бывают пространственные и плоские механизмы
Звено – деталь или несколько деталей механизма, движущихся как одно целое
Механизмы классифицируются по виду звеньев:
Ø С твердыми телами
Ø С упругими звеньями (пружины, торсионы и т.д.)
Ø Винтовые
Ø Храповые
Ø Гидромеханизмы
Ø Пневмомеханизмы
И т.д.
Кинематическая пара – подвижное соединение двух звеньев взаимоограничивающее их движение.(одно из звеньев может быть неподвижным – стойка)
Кинематические пары классифицируются :
1.По виду контакта : на низшие и высшие
а) У высших контакт по (.) или по линии.
б) У низших контакт по поверхности.
(Достоинство а): различные законы движения, недостаток - велики удельные нагрузки)
2.По степеням свободы: (По числу ограничений накладываемых на относительное движение звеньев)
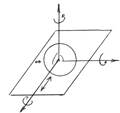 а).I Класс – шар на плоскости
а).I Класс – шар на плоскости
5 ст. свободы (высшая кинемат. Пара)
| - изобр. по ГОСТ |
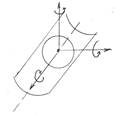 б). II Класс
б). II Класс
4 ст. свободы
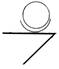
| - изобр. по ГОСТ |
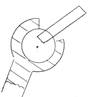 в). III Класс – сферический шарнир
в). III Класс – сферический шарнир
3 ст. свободы
| - изобр. по ГОСТ |
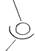
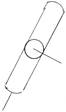 г). IV Класс – 2 ст. свободы
г). IV Класс – 2 ст. свободы
Внешняя плоская пара
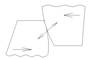
| - изобр. по ГОСТ |
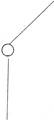
д). V Класс – 1 ст. свободы
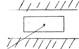
| - изобр. по ГОСТ |
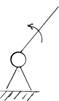
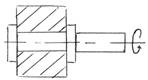
Кинематическая цепь : Кинематические пары между собой связываются; поэтому связанная совокупность звеньев, образующих кинематические пары называется
кинематической цепью.
Классифицируются кинематические цепи:
1) Пространственные и плоские
2) Простые и сложные (простая , когда звено входит не более чем в две кинематические пары)
3) Замкнутые и разомкнутые
Примеры:
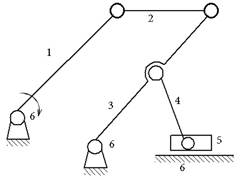
| Пространственная, простая разомкнутая | Плоская, сплошная замкнутая |
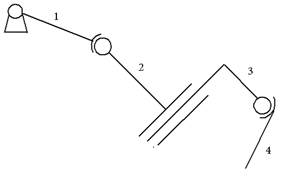
| 
|
Подавляющее большинство механизмов состоит из замкнутых кинематических цепей.
Структурная формула кинематической цепи:
Она отвечает на вопрос : сколько степеней свободы имеет данная кинематическая цепь? Какова ее подвижность?
Рассмотрим любую кинематическую цепь из k-звеньев. Кинематические пары цепи обозначим P1 – кп 1 кл; P2 – кп 2 кл; …. P5 – кп 5 класса.
Без учета кинематических пар, k звеньев имеют 6-k степеней свободы
Тогда:
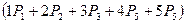 - Общее количество ограничений кинем. цепей
- Общее количество ограничений кинем. цепей
Подвижность цепи: 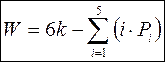 (1) – общая структурная
(1) – общая структурная
формула
пространственной кинемат. цепи
Если одно звено неподвижно, то 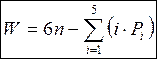 (2) , где n – число
(2) , где n – число
подвижных звеньев
Для плоской цепи: 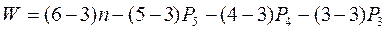
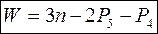 - Формула Чебышева
- Формула Чебышева
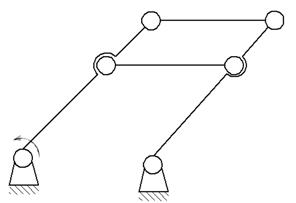
Из вышесказанного можно дать структурное определение механизма: Механизмом называется замкнутая кинематическая цепь с одним неподвижным звеном в которой при заданном законе движения одного или нескольких звеньев, называемых ведущими, все остальные звенья (ведомые) имеют вполне определенное движение
В механизме могут быть избыточные связи называемые пассивными:
|
Структурный анализ механизма включает в себя:
1. Определение структуры механизма
2. Количества подвижных звеньев
3. Количества кинематических пар и класс кинематических пар
4. Определение подвижности механизма
5. Определение количества ведущих звеньев
Тема №2 Рычажные механизмы.
Отличительные особенности – в их состав входят только низшие кинематические пары. Для пространственных рычажных механизмов пары 5 кл. (вращат. и поступат.)
4 кл. (цилиндрические ) 3 кл. – сферические механизмы. Для плоских механизмов – только пары 5го класса
Достоинства: 1. Высокая нагрузочная способность (винтовые пары по поверхности)
2. Относительная простота и дешевизна
Недостатки: 1. Небогатый выбор движений на выходе (возвратно-поступательное или вращательное)
2. Сложность метрического синтеза, т.е. расчета размеров механизма при котором достигается требуемый закон движения на выходе.
О классификации рычажных механизмов
В основу классификации положен структурный признак. Любой рычажный механизм состоит из 3-х видов элементов.
1. Одного (весьма редко нескольких) исходного механизма (подвижность его ω = 1)
2. Любого числа наиболее простых кинематических цепей с нулевой подвижностью (ω = 0). Такая цепь называется группой Ассура.
3. Любого числа пассивных звеньев (элемент необязательный и может отсутствовать).
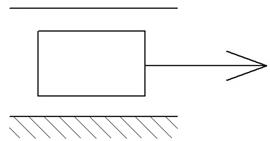
Исходный механизм может быть только двух видов:
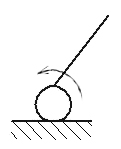
| 
|
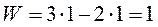
Исходных механизм I класса. I-го порядка, в каждом сложном механизме.
Классификация структурных групп
Структурная группа – это простейшая кинематическая цепь обладающая нулевой подвижностью.
Структурная формула группы Асура:
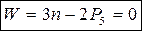 (1)
(1)
Для плоских механизмов могут быть только пара 5-го класса (частный случай 1 P4 в 2 P5)
Из (1) следует
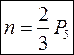 - число подвижных звеньев, входящих в группу (только четное , т.е. n = 2, 4, 6, 8
- число подвижных звеньев, входящих в группу (только четное , т.е. n = 2, 4, 6, 8
Также следует, что 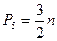 - число кинематических пар 5го класса – кратно трем (3, 6, 9, 12)
- число кинематических пар 5го класса – кратно трем (3, 6, 9, 12)
Отсюда следуют:
Признаки группы Ассура:
1. В группе Ассура должно быть четное число звеньев;
2. Они входят или могут входить в число кинематических пар, кратное 3-м; 3;6;9;12
3. Группу Ассура нельзя мысленно разбить на более простые цепи с W = 0
4. Если группу Ассура со свободными элементами пар присоединить к одному и тому же звену (стойке) то получится жесткая ферма.
Все группы Асура делятся на 3 класса (2,3,4)
(1 кл. отдан исходному механизму)
I Группы 2-го класса(диады)
n=2 , P5 = 3- все эти группы являются 2-х поводковыми, т.е. 2-й порядок.
Поводок – звено имеющее свободный элемент кинематической пары
Имеется 5 видов диад: (идет замена вращательной пары поступательными)
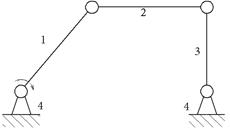
1 вид
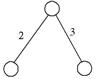 В – В – В
(В - вращательная пара)
В – В – В
(В - вращательная пара)
| 
|
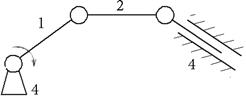
2 вид
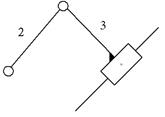 В – В – П
(П – поступательная пара)
В – В – П
(П – поступательная пара)
| 
|
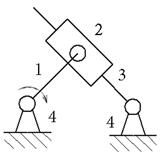
3 вид
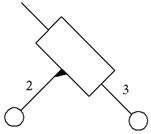 В – П – В
В – П – В
| 
|
4 вид
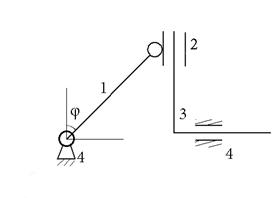
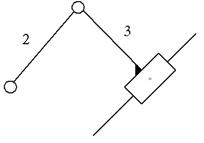 В – П – П
В – П – П
| 
|
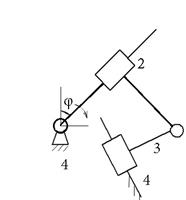
5 вид
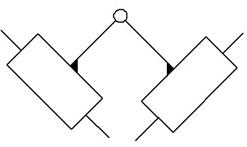 П – В – П
П – В – П
| 
|
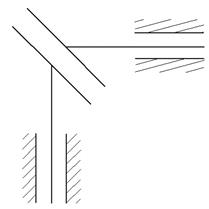
6 вида не существует, т.к. он является исключением (П-П-П) после присоединения к стойке не образует ферму, а преобразуется в клиновой механизм
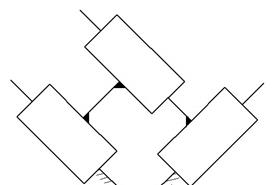
| = | 
|
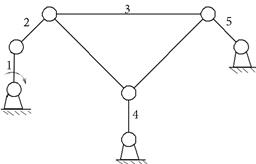
II Группы 3-го класса (триада – трехповодковая группа)
Характеристический признак : наличие хотя бы одной сложной цепи.
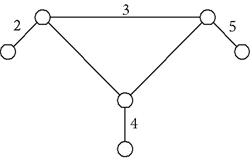 ω = 0
ω = 0
|  ω = 1
ω = 1
|
| 3-й класс 3-й порядок N = 4 P5 = 6 |
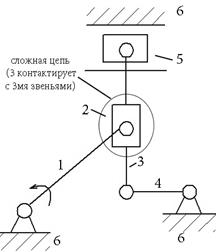
Любая вращательная пара может быть заменена на поступательную , кроме одной (одну надо оставить)
|
III Группы 4-го класса
Характеристический признак: наличие замкнутого контура звеньев.
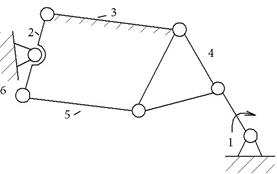
| 4-й класс 2-й порядок n=4 |
Структурный анализ рычажного механизма
1. Определить подвижность и выделить исходный (главный) механизм
2. Мысленно отделить остающуюся цепь от исходного механизма и разбить на гр. Ассура.
3. Определить класс и порядок каждой группы.
4. Всему механизму присвоить класс и порядок старшей группы.
Синтез осуществляется путем присоединения к исходным механизмам любого числа структурных групп
О кинематическом анализе (синтезе) рычажных механизмов
Задача : определение кинематических параметров механизма (угловых или линейных перемещений , скоростей, ускорений звеньев или отдельных точек)
Замечание: Чем выше класс и порядок механизма тем сложнее его кинематический анализ
Методы:
1. Экспериментальные: дают наиболее достоверные результаты.
Недостатки: требуется лабораторное оборудование (измерительное, регистрирующая аппаратура, образец механизма).
2. Графические : планы механизмов, скоростей, ускорений; графическое интегрирование, дифференциальное и т.д.
Достоинство: простота, наглядность
Недостатки: необходимость выполнения построений графически, с применением чертежных инструментов в масштабе, иногда невысокая точность.
3. Аналитические: не требуют графических построений, обеспечивают сколь угодно точный результат.
Недостатки: громоздкость расчетов.
Тема №3 План скоростей и ускорений.
Дано : ω1 = 0
Размеры всех звеньев
Определить : Кинематические параметры
1. План скоростей – геометрическое построение, представляющее совокупность векторов, отображающих скорость любой точки механизма (последовательно определяем линейную скорость и w любой точки и звена механизма)
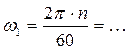
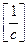
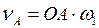
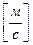
Как строить план скоростей?
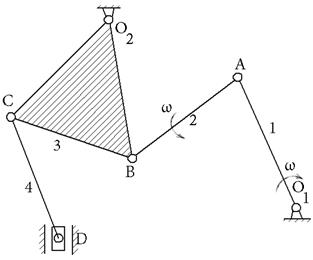
| |
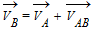 (1)
┴BO2 ┴DA ┴AB (1)
┴BO2 ┴DA ┴AB
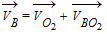 (2)
┴BO2 0 ┴ BO2 (2)
┴BO2 0 ┴ BO2
| ∆ - изв. величина ↑ - изв. направление Pv – полюс плана (Кv) – масштабный коэффициент плана скоростей |
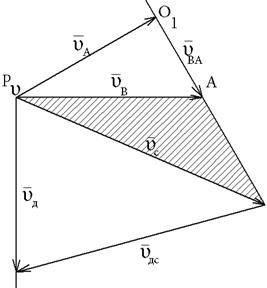
| 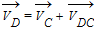 (3)
Вертик. ┴O2C ┴ DC (3)
Вертик. ┴O2C ┴ DC
|
Правила:
1. План скоростей звена является геометрическим местом концов векторов скоростей всех точек данного звена.
2. План скоростей звена подобен звену и повернут по отношению к этому звену на 90 градусов
Зная линейные скорости любых точек определяем угловые скорости любого звена:
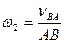 ;
; 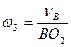 ;
; 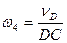 ; Направление вращения звена, т.е. знак ω2 , ω3, ω4 определяется просто
; Направление вращения звена, т.е. знак ω2 , ω3, ω4 определяется просто
План ускорений
При ω1 = const:
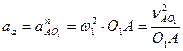
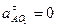 , т.к.
, т.к. 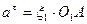 но
но 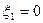
Решение: векторный замкнутый многоугольник
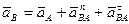 (4)
(4)
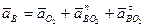 (5)
(5)
Здесь: 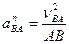 ;
; 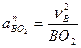
Масштабный коэффициент 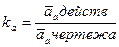
PA – полюс плана ускорений
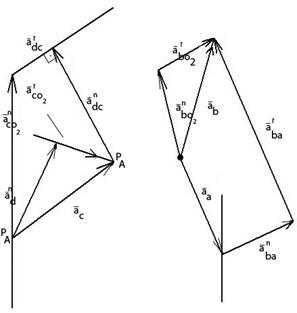
| Угловое ускорение из 1-го многоугольника
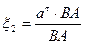 , , 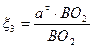
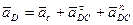 (6) (6)
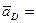 знаем направление знаем направление
|
Метод позволяет определить угловое ускорение звена 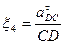
Аналитические методы
1) метод векторных контуров
Механизм представляется в виде одного или нескольких замкнутых векторных контуров (это можно сделать т.к. звено, аналогично вектору, имеет величину и направление)
Метод удобен когда необходимо определить угловые параметры: угловое ускорение, скорость, узловые перемещения звена
Дано: l1, l2, l3,l4
ω1 = const; φ1
Найти: φ2 φ3 ω2 ω3 ξ2 ξ3
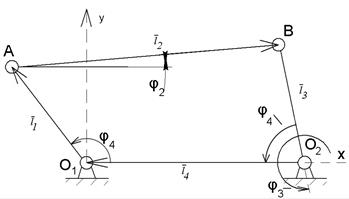
| 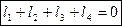 (1) (1)
|
Проецируем на оси координат:
На ось х: 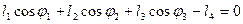 (2)
(2)
На ось у: 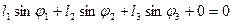 (3) решая их, найдем φ2 и φ3
(3) решая их, найдем φ2 и φ3
Продиффиринцируем систему помня, что 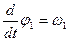 ;
; 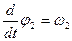 ;
; 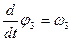
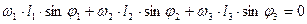 (4)
(4)
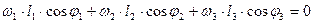 (5) найдем ω2 и ω3
(5) найдем ω2 и ω3
Дифференцируем 2-й раз, учитывая, что 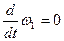 (т. к. ω1 = const)
(т. к. ω1 = const)
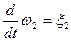 ;
; 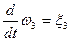
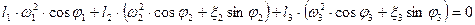 (6)
(6)
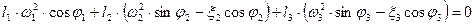 (7) найдем ξ2 и ξ3
(7) найдем ξ2 и ξ3
2) Метод преобразования координат (повернутых координат)
Пригоден для определения линейных кинематических параметров характерных точек ( в него входит метод векторных контуров; угловые параметры φi ωi ξi известны )
Суть метода : с каждым звеном механизма (включая стойку) связывается (жестко) своя система координат движущаяся вместе со звеном
Обозначим координаты точки S , X22 и Y22 - const (конструктивные параметры) φ2 известно из метода векторных контуров.
Связь между системами координат:
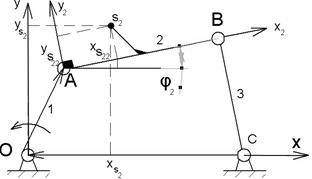
| Обозначим 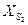 и и 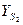 - - 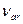 (именно они определяют положение точек S2 на плоскости) (именно они определяют положение точек S2 на плоскости)
|
Тогда связь между координатами:
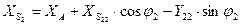
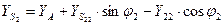
Запишем в матричной форме
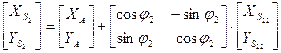 (8)
(8)
Дифференцируем (8) два раза последовательно по времени, получим:
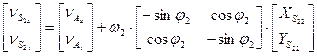 (9)
(9)
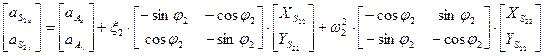 (10)
(10)
(8); (9); (10) позволяют последовательно определить все величины 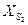 ;
; 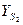 ;
; 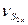 ;
; 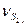 ;
; 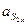 ;
; 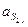 и далее определить кинематические параметры следующего звена. Работает только с методом векторного контура, т.к. необходимы угловые параметры.
и далее определить кинематические параметры следующего звена. Работает только с методом векторного контура, т.к. необходимы угловые параметры.
Два последних метода удобны для расчетов на ЭВМ, для расчета «в ручную» они не удобны. Можно перебирать множество вариантов чтобы получить механизм удовлетворяющий выдвигаемым требованиям.
О синтезе рычажных механизмов (замечание)
Дано: структурная схема механизма, его функция положения или её производная
Найти : размеры звеньев механизма, при котором эта функция обеспечивается
Решение:
1) Выполняется элементарно
2) Может быть выполнено очень приближенно
3) Решение невозможно вообще
1) Условие существования кривошипа
В состав многих механизмов входит шарнирный 4-х звенник. (возникает вопрос – когда он может совершить полный оборот?)
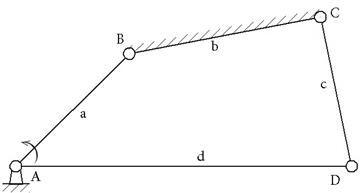
| Дано: AB = a; a<b BC = b; a<c CD = c; a<d DA= d; d>b; d>c Найти при каких соотношениях a,b,c,d. Звено a совершает оборот |
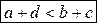 (11)
(11)
1. Если стойка b или d, то a – кривошип; b или d – шатун; с – коромысло
2. Если стойкой является a, то b;d – крипошипы, с – шатун
3. Если стойкой является с, то нет кривошипа
Если заменить (11) равенством, то механизм превращается в предельный механизм. В одном из положений все звенья вытягиваются вдоль одной прямой – мертвое положение (неопределенное)
Теорема Грасгофа: Для того чтобы звено a было кривошипом, необходимо и достаточно, чтобы оно было наименьшим из всех звеньев и сумма его длины и длины любого из звеньев была меньше суммы длин оставшихся звеньев.
2) Условие рациональной передачи сил
Динамическое условие, учитывается при проектировании любой кинематической схемы.
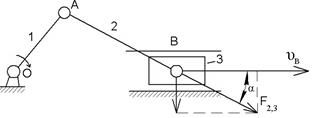
Понятие угла давления (α) - угол между направлением вектора силы F, передающим усилие с одного звена на другое и направлением вектора скорости точки приложения силы (силой трения пренебрегаем)
| 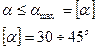
|
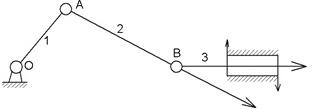
| Если 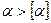 возникает большой изгибающий момент, возрастают потери возникает большой изгибающий момент, возрастают потери
|
Тема №4 Кулачковые механизмы.
Присутствует 1 звено (по очертанию напоминает кулачок) имеющее профиль переменной кривизны.
Назначение – преобразование простого движения на входе (вращение, пост. Движение), в более сложное движение на выходе, включая выстои (кулачек движется, звено неподвижно). Поэтому кулачки широко используются в управляющих механизмах.
Используется вращательное движение с ω = const (Иногда кулачек неподвижен – копир)
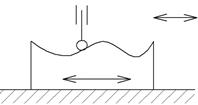
|
Типы кулачковых механизмов : плоские и пространственные, наиболее распространены первые.
Достоинства кулачковых механизмов:
1) Широкий набор возможных движений на выходе (определяется формой кулачка)
2) Простота перехода на другой закон движения на выходе (смена кулачка)
3) Простота согласования работы нескольких механизмов (распределит. Вал)
4) Простота синтеза кулачковых механизмов (если график S(φ) известен то получим профиль кулачка)
Недостатки
| ↓ | → | ┴ | → | 
|
1) Невысокая нагрузочная способность из за наличия высшей кинематической пары (контакт по точке или линии) Можно несколько улучшить
2) Необходимость замыкания кинематической пары (силовое, геометрическое)
3) Сложность изготовления кулачка
Кулачковый механизм состоит из 3х звеньев: стойка, кулачок(ведущее звено), ведомое звено(толкатель или коромысло , в зависимости от вида движения)
Основные элементы кулачка и кулачкового механизма
(на примере механизма с толкателем)
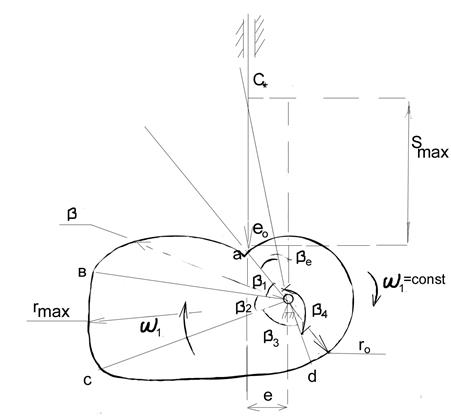
e – эксцентриситет
1) ab – участок профиля удаления
ρ - радиус-вектор кулачка,
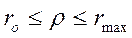
ro- радиус базовой окружности
2) bc – участок профиля дальнего выстоя
(кулачек вращается, ведомое звено неподвижно). 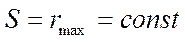
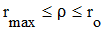 3) cd – участок профиля возвращения
3) cd – участок профиля возвращения
4) da – участок профиля ближнего выстоя 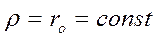
(кулачок вращается, ведомое звено не подвижно)

точка 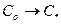 верхнее положение при
верхнее положение при 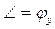
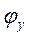 - угол удаления, повороты кулачка соответствующие выполняемым толкателем фазы удаления (фазовые узлы кул. мех.)
- угол удаления, повороты кулачка соответствующие выполняемым толкателем фазы удаления (фазовые узлы кул. мех.)
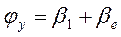 ;
; 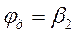 ;
; 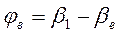 ;
; 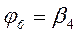
Дата добавления: 2015-06-17; просмотров: 3867;
