II.ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. 4 страница
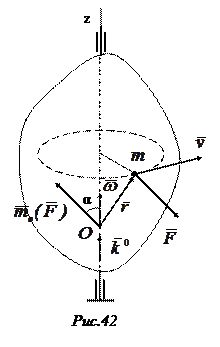
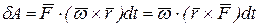 ,
,
так как по свойству смешанного произведения векторов
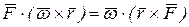 .
.
Как было показано в статике 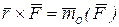 —момент силы
—момент силы 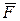 относительно полюса
относительно полюса 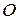 , поэтому
, поэтому
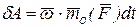 .
.
По определению скалярного произведения двух векторов
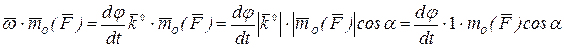 .
.
Здесь учтено, что 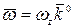 , где
, где 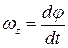 —алгебраическая угловая скорость,
—алгебраическая угловая скорость, 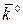 —орт оси вращения. Тогда
—орт оси вращения. Тогда
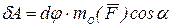 .
.
Опираясь на полученную в статике зависимость между моментом силы относительно полюса и оси
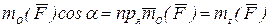 .
.
Окончательно
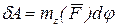 ,
,
т. е. элементарная работа силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси, равна произведению момента этой силы относительно оси вращения на элементарный угол поворота.
Работа этой силы на конечном повороте тела определяется равенством
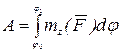 .
.
Если 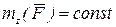 , то
, то
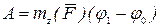 ,
,
т. е. работа равна моменту относительно оси вращения, умноженному на угол поворота тела.
4.4.7. Кинетическая энергия материальной точки и механической системы.
Кинетической энергией материальной точки называется скалярная (всегда положительная) величина, равная половине произведения массы этой точки на квадрат её скорости:
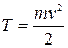 .
.
Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы:
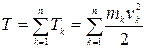 .
.
Кинетическая энергия механической системы—величина всегда положительная, равна нулю только в том случае, когда скорости всех точек механической системы равны нулю.
Единицей кинетической энергии в СИ является джоуль: 1 Дж=1Н·м.
4.4.9. Кинетическая энергия твердого тела.
1. Поступательное движение твердого тела.
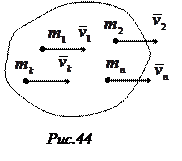 При поступательном движении твердого тела скорости всех его точек геометрически равны между собой (рис. 44):
При поступательном движении твердого тела скорости всех его точек геометрически равны между собой (рис. 44):
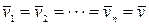 ,
,
где 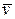 —общая скорость для всех точек тела.
—общая скорость для всех точек тела.
Кинетическая энергия тела определяется формулой (4.74):
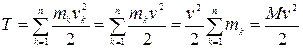 ,
,
где 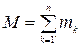 —масса тела.
—масса тела.
Кинетическая энергия тела, совершающего поступательное движение, равна половине произведения массы тела на квадрат его скорости, т. е.
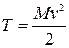 .
.
2. Вращение твердого тела вокруг неподвижной оси.
 При вращении твердого тела вокруг неподвижной оси (рис.45) скорость точек тела определяется выражением
При вращении твердого тела вокруг неподвижной оси (рис.45) скорость точек тела определяется выражением 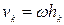 , где
, где 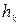 —расстояние от точки тела
—расстояние от точки тела
до оси вращения, а 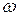 —угловая скорость тела, одинаковая для всех его точек. Кинетическую энергию твердого тела определяем по формуле (4.74)
—угловая скорость тела, одинаковая для всех его точек. Кинетическую энергию твердого тела определяем по формуле (4.74)
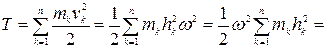
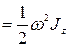 ,
,
где 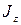 —момент инерции тела относительно оси вращения
—момент инерции тела относительно оси вращения 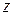 . Следовательно, кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела, т. е.
. Следовательно, кинетическая энергия тела, вращающегося вокруг неподвижной оси, равна половине произведения его момента инерции относительно оси вращения на квадрат угловой скорости тела, т. е.
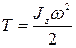 .
.
4.4.10. Теорема об изменении кинетической энергии материальной точки.
Теорема.Изменение кинетической энергии материальной точки на конечном перемещении равно сумме работ сил, действующих на точку на этом перемещении, т. е.
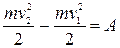 .
.
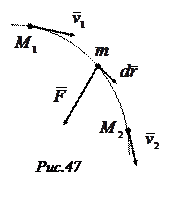 Доказательство. Рассмотрим материальную точку массой
Доказательство. Рассмотрим материальную точку массой 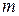 , движущуюся
, движущуюся
под действием сил 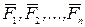 . Обозначим
. Обозначим 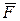 —равнодействующую этой системы сил (рис.47). Установим зависимость между работой, совершаемой приложенными к точке силами (работой равнодействующей) на конечном перемещении из положения
—равнодействующую этой системы сил (рис.47). Установим зависимость между работой, совершаемой приложенными к точке силами (работой равнодействующей) на конечном перемещении из положения 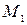 в положение
в положение 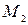 , и изменением кинетической энергии точки на этом перемещении.
, и изменением кинетической энергии точки на этом перемещении.
Основное уравнение динамики точки
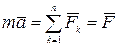 .
.
Умножим обе части этого уравнения скалярно на вектор элементарного перемещения 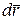 :
:
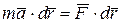 ,
,
или
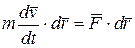 ,
, 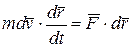 ,
,
Учитывая, что 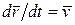 —скорость точки:
—скорость точки:
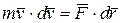 .
.
Правая часть в этом равенстве 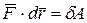 —элементарная работа. Так как
—элементарная работа. Так как
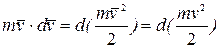 ,
,
то окончательно
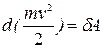 .
.
Формула (4.87) выражает теорему об изменении кинетической энергии материальной точки в дифференциальной форме: дифференциал кинетической энергии материальной точки равен элементарной работе сил (равнодействующей сил), действующих на эту точку.
Проинтегрировав обе части равенства (6.87) в пределах интегрирования, соответствующих начальному 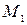 и конечному
и конечному 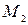 положениям точки:
положениям точки:
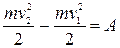 ,
,
и теорема доказана.
В приложениях весьма полезна другая формулировка доказанной теоремы. Разделим обе части (4.87) на 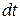 и учтем, что
и учтем, что 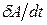 —мощность. Тогда
—мощность. Тогда
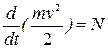 ,
,
т. е. производная по времени от кинетической энергии материальной точки равна мощности действующих на эту точку сил.
11. Теорема об изменении кинетической энергии механической системы.
Теорема.Изменение кинетической энергии механической системы при её перемещении из первого положения во второе равно сумме работ внешних и внутренних сил, действующих на систему, на этом же перемещении, т. е.
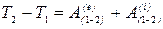 .
.
Дата добавления: 2015-04-21; просмотров: 2119;
