Розрахунок моментів інерції деяких тіл. Теорема Штейнера

Момент інерції тіла залежить не тільки від маси тіла, а і від її розподілу відносно осі обертання. Тому одне і теж тіло має різні моменти інерції відносно різних осей обертання. Розглянемо ряд прикладів розрахунку моменту інерції, користуючись його означенням (4.40).

a)момент інерції матеріальної точки. Задана маса m і радіус 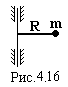обертання R (рис.4.16). Знайти J.

Згідно з означенням (4.40) моменту інерції .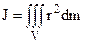

В нашому випадку r = R = const.

Тому 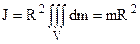. (4.45)

б) момент інерції обруча (труби)відносно осі, яка проходить через його центр і перпендикулярна площині обруча. Задана маса m і радіус 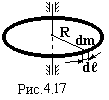обруча R (рис.4.17). Знайти J.

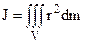. r = R = const.

Тому 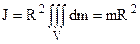. (4.46)

в) Момент інерції диска (циліндра)відносно осі, яка співпадає з віссю циліндра. Задана маса диска m і його радіус R (рис.4.18). Знайти J.

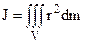. Виберемо елемент dm у вигляді труби радіусом r з товщиною стінки dr і довжиною b, яка дорівнює товщині диска (висоті циліндра). Маса цієї труби 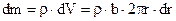. Густина 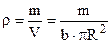. Тому маємо

.

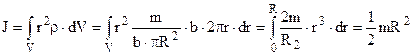Таким чином, момент інерції обруча (циліндра) 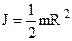. (4.47)

Видно, що порівнюючи з обручем (трубою) маса диска (циліндра) розподілена в цілому ближче до осі обертання. Тому і одержаний момент інерції менший.

г) момент інерції довгого тонкого стержнявідносно осі, яка перпендикулярна до нього і проходить через середину стержня. Задані маса m стержня і його довжина (рис.4.19). Знайти J.

Виберемо елемент dm у вигляді частини стержня довжиною dr, який віддалений від осі на відстань r.

Його маса dm порційна довжині і дорівнює 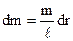. Момент інерції стержня

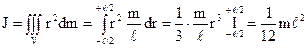. (4.48)

д) момент інерції кулі відносно діаметра. Задана маса m і радіус R. Момент інерції кулі 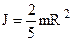. (4.49)

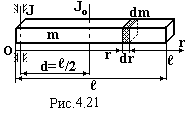
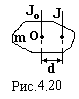
Для розрахунку моментів інерції тіл відносно осей, які не проходять через центр маси тіл (рис.4.20), застосовується теорема Штейнера: момент інерції J тіла відносно будь-якої осі дорівнює сумі моменту інерції J_o цього тіла відносно осі, яка проходить через центр маси О тіла та паралельна заданій, і добуткові маси m тіла на квадрат відстані d між цими осями

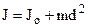. (4.50)

Впевнимося у справедливості цієї теореми на прикладі розрахунку моменту інерції довгого стержня відносно осі, яка перпендикулярна до стержня і проходить через його край (рис.4.21). Безпосереднє інтегрування, як і у прикладі 4) дає

.

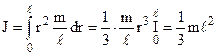По теоремі Штейнера, враховуючи (4.48), одержуємо

(4.51)

такий же результат, як і безпосереднім інтегруванням.