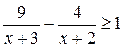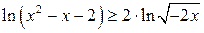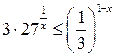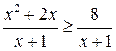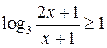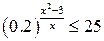MathCad. Розв’язання рівнянь, систем рівнянь та нерівностей.

Аналітичний розв’язок можна знайти для дуже обмеженої кількості задач. Ми можемо розв’язувати рівняння із змінними невисоких степенів які спеціально підібрані в підручнику. Чисельно ж можна розв’язати будь яке рівняння. Досвід показує, що простіші рівняння краще розв’язувати символьно, а більш складні – чисельно. Рідше – трапляються складні рівняння, які досить важко розв’язати чисельно і символьно, тоді використовують графічний метод розв’язання рівнянь. Він є досить трудоємким, але забезпечує точність не гіршу ніж чисельний процесор. Для цього використовують інструменти панелі Graph.

1. Аналітичне розв’язання рівнянь.

Для аналітичного розв’язання рівнянь в системі MathCad є спеціальний оператор Solve (Розв’язати) панелі Symbolic (Символьні).

Для того, щоб знайти корені рівняння за допомогою оператора Solve потрібно:

1. Вводимо оператор Solve з панелі Symbolic.
2. В лівому маркері задаємо вид рівняння, яке потрібно розв’язати. В якості „=” потрібно ввести знак рівності з панелі Boolean (Ctrl+”=”).

!!!! Також в лівий маркер можна вводити ім’я функції. У цьому випадку програма знайде нулі функції. Форма запису рівняння через функцію зручне у випадку, коли вона має велику довжину.

1. В правий маркер вводимо змінну, відносно якої потрібно виконати розв’язання рівняння.

Якщо рівняння має декілька розв’язків, то оператор Solve подає результат у вигляді вектора (матриця - стовпець).

Розглянемо найпростіший приклад:

Розв’язати рівняння: x²-2x-3=0. Для цього: Вводимо оператор Solve. Знак рівності вводимо з панелі

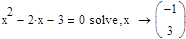Boolean.

Найкраще MathCad знаходить корені алгебраїчних поліномів. Причому, знаходяться всі корені, як дійсні, так і уявні. Їх загальне число дорівнює найвищому степеню полінома. В алгебрі доведено, що аналітичні вирази існують тільки для поліномів 5го степеня. Якщо символьний процесор з’ясує, що степінь полінома вищий ніж 4, то буде задіяно напівчисельний метод. В результаті корені будуть знайдені, але не в формі виразів, а у вигляді десяткових чисел. Розглянемо дану різницю на прикладі: (х+2)²-(х+13)³=1.

Приклад:

Зверніть увагу на те, що рівняння має один дійсний розв’язок, і два комплексних.

Приклад:

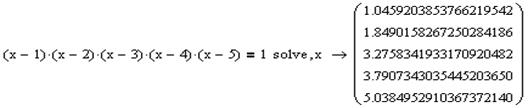
Так як степінь даного полінома – 5, а це вище ніж 4, то застосовано чисельний метод. І результат отримано у вигляді десяткових чисел.

У випадку, коли відповідь є надто громіздкою, використовують оператор Float. Він служить для задання точності виводу результату.

Наприклад: Приклад:

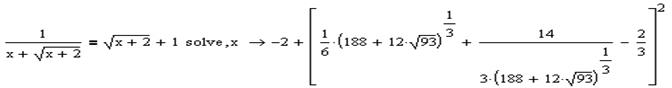
Застосуємо оператор Float із точністю 10:

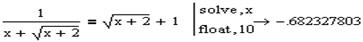Це означає, що відповідь: -0,682327803.

Приклад:

Розв’язати рівняння з параметром:

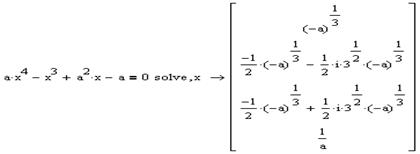Також бачимо, що рівняння має три корені. Один дійсний та два комплексних.

Розв’язання логарифмічних рівнянь.

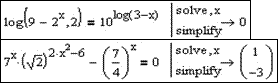Для розв’язання логарифмічних рівнянь слід пам’ятати, що натуральний логарифм в MathCad задається функцією ln, а десятковий – log. Для задання логарифма з основою х також служить функція log. Але в цьому випадку вона приймає два параметри: перший відповідає величині від якої потрібно знайти логарифм, другий призначений для вказування основи. Розв’язуючи логарифмічні та показникові рівняння зазвичай отримуємо складну відповідь. Для того, щоб привести її до більш зручного вигляду слід застосовувати разом з оператором Solve оператор Simplify. Наприклад:

Розв’язання тригонометричних рівнянь.

Із всіх видів рівнянь, тригонометричні рівняння MathCad розв’язує найгірше. Як відомо, більшість таких рівнянь мають нескінченну кількість коренів, які записуються за допомогою спеціальних виразів, наприклад: коренем рівняння sin(x)=0 є π+πk, (де k є Z(ціле число)). MathCad знаходить корені лише на проміжку одного періоду функції, заданої в рівнянні. Також, MathCad досить часто робить помилки у розв’язанні тригонометричних рівнянь, особливо, якщо таке рівняння містить параметри. Тому на практиці краще будувати графіки таких рівнянь, або намагатися максимально спростити рівняння. Розглянемо два таких приклада:

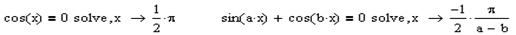
2. Чисельне розв’язання рівнянь.

- Функція root

На практиці часто приходиться мати справу з рівняннями, які містять в собі різного роду функції, і які розв’язати символьно практично неможливо. На практиці такі рівняння розв’язують підбором і підстановкою, а в MathCad для цього існує чисельний метод розв’язання рівнянь.

Для чисельного пошуку розв’язків алгебраїчних рівнянь з одним невідомим, в MathCad існує спеціальна функція root (корінь). Знаходиться в Функціях, в розділі Solving. Якщо визначена лише одна точка наближення до кореня, пошук розв’язку буде здійснюватися так званим методом січних. Якщо ж задано інтервал, на якому локалізовано розв’язок, то його пошук буде здійснено за із застосуванням методу поділу навпіл (або методу Больцано).

Якщо потрібно знайти корінь деякого рівняння, і відомо інтервал, на якому локалізований цей корінь, то найкраще використовувати функцію root з чотирьма аргументами: root (f(x),x,a,b), де f(x) – функція, що визначає рівняння, x – змінна, a,b – межі інтервалу локалізації. Обов’язковою умовою є те, що:

- значення функції на кінцях інтервалів повинні бути з протилежними знаками.

- функція f(x) повинна бути обмеженою і неперервною на проміжку (a,b).

- На проміжку локалізації повинен бути лише один корінь.

Приклад чисельного розв’язання рівняння методом Больцано.:

Розв’язати рівняння cos(2x)=0 на проміжку від 0 до π/3.

Розв’язання: При чисельному розв’язанні рівнянь бажано завжди будувати графік функції. Це допоможе уникнути помилок і правильно визначити потрібний інтервал локалізації коренів. Побудуємо графік нашої функції:

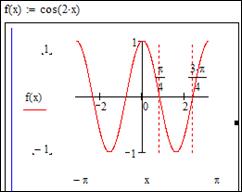Змінимо межі по ОХ від (-π;π) для зручності. Поставимо маркери в точках π/4 та 3π/4. Очевидно, що всі корені цього рівняння рівняння мають вигляд: 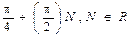, де R – множина цілих чисел. Подивимось, чи знайде функція rootкорені даного рівняння на вказаному проміжку.

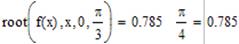
Корінь визначено вірно.

- Функція polyroots

У тому випадку, коли рівнянні задане алгебраїчним поліномом, в MathCad є спеціальна функція пошуку коренів polyroots (V). Де V– вектор, що складений з коефіцієнтів полінома. V=(х⁰,х¹,х²,…,хⁿ) де n – показник степеня. ((в MathCad записуємо зверху вниз від 0 до n)). Відповідь видається у вигляді вектора, що містить як дійсні, так і комплексні корені. Знаходиться в Функціях, в розділі Solving.

Приклад знаходження коренів полінома:

Знайти корені рівняння такого виду: х⁴+х³+х-10=0

Розв’язання: Створюємо вектор коефіцієнтів і використовуємо функцію polyroots.

Бачимо, що рівняння має два дійсних кореня. Всі розв’язки записані у формі вектора в порядку зростання зверху вниз.

Замість того, щоб записувати коефіцієнти вручну, в MathCad існує можливість здійснити такий запис автоматично. Крім того програма може автоматично спростити поліном. Для цього в MathCad є спеціальний оператор Coeffs (коефіцієнти) панелі Symbolic (символьні).

Розглянемо наступний приклад на використання оператора Coeffs:

Розв’язати рівняння: (x²+x-3)²+(x-10)³ .

Розв’язання: Розв’яжемо рівняння за допомогою функції polyrootsі для створення вектора з коефіцієнтів використаємо оператор Coeffs.

Бачимо, що програма спростила рівняння автоматично і побудувала вектор його коефіцієнтів. Рівняння має два дійсних кореня і всі корені розміщені в порядку зростання зверху вниз.

3. Графічне розв’язання рівнянь.

Графічне розв’язання рівняння – це метод розв’язання, який заклечається у визначенні по графіку функції, при яких величинах аргументу, дана функція приймає значення рівне нулю. Графічний метод є незамінним у тому випадку, коли рівняння неможливо розв’язати ні аналітично, ні чисельно. Це зазвичай трапляється у тому випадку, коли функції приймають не неперервний, а дискретний набір значень. Для розв’язання будуємо графік функції, та за допомогою інструментів Zoom та Trace визначаємо потрібні нам значення.

1. Розв’язання систем лінійних рівнянь.

Всі методи розв’язання систем лінійних алгебраїчних рівнянь можна розділити на дві основні групи.

До першої відносяться так звані прямі (матричні) методи: Гаусса, Крамера. До другої групи відносять ітераційні методи.

Для знаходження коренів систем лінійних рівнянь методом Крамера в Mathcad існує спеціальна функція lsolve(M,v), де M –матриця коефіцієнтів,v –вектор правих частин. Особливістю функції lsolveє те, що вона може знаходити і чисельні і аналітичні розв’язки. Розглянемо приклад.

Розв’язати систему лінійних рівнянь з параметром наступного виду:

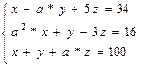Для розв’язання використаємо метод Крамера.

Для цього створимо матрицю коефіцієнтів, вектор правих частин, і застосуємо функцію lsolve з оператором символьного виводу.:

Для знаходження коренів систем лінійних рівнянь методом Гауса в Mathcad існує функція rref(M),деM –матриця, отримана злиттям матриці коефіцієнтів і вектора правих частин. Знаходиться в розділі функцій Vector and Matrix.

Розглянемо приклад:

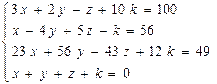Розв’язати систему лінійних рівнянь методом гауса:

Будуємо матрицю коефіцієнтів і вектор правих частин. Застосовуємо функцію злиття матриць augment. До отриманої матриці застосовуємо функцію rref.

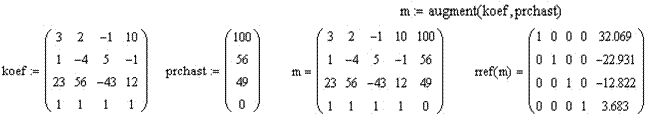
1. Аналітичне розв’язання систем нелінійних рівнянь.

1. Отримати аналітичний розв’язок систем рівнянь в MathCad можна за допомогою оператора Solve. Для цього потрібно ввести систему рівнянь у вигляді вектора в його лівий маркер, а в правий – змінні, значення яких потрібно знайти. Приклад:

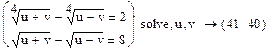
2. Для аналітичного розв’язання систем нелінійних рівнянь можна використовувати так званий обчислювальний блок. Обчислювальним блоком в MathCad називають систему із ввідного слова Given (дано) і функції тої математичної операції, яку потрібно виконати. Для того, щоб розв’язати систему рівнянь, використовують обчислювальний блок Given (Дано) – Find (Знайти).Для використання Given – Findпотрібно виконати таку послідовність дій:

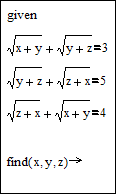1. Набрати ввідне слово Given.
2. Строго під ввідним словом задати систему рівнянь так, як це робимо на папері. В якості знака рівності використовуємо логічну рівність.

3. Із розділу Solving (розв’язання) у списку функцій вибираємо функцію Find (х1,х2,…). В дужках задаємо змінні у тому порядку, в якому повинні бути розміщені відповідні їм корені.

4. В якості оператора виводу результату використовуємо «→». Якщо поставити оператор чисельного виводу «=», то для розв’язання системи буде задіяно один з чисельних алгоритмів.

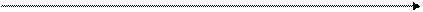Розглянемо приклад розв’язання системи рівнянь за допомогою блоку Given – Find. Приклад:

6 Чисельне розв’язання систем нелінійних рівнянь.

Як і у випадку із звичайними рівняннями, ми звертаємося до чисельних методів лише тоді, коли аналітично розв’язати рівняння неможливо. Для чисельного розв’язання систем рівнянь в MathCad служить той самий блок Given – Find. Тільки спосіб задання його дещо інший.:

1. Обов’язково для кожної змінної повинно бути визначено початкове наближення наприклад: x:=10^-3 y:=10³ z:=1.

2. Для виводу результату потрібно поставити оператор чисельного виводу “=”.

При розв’язанні рівнянь за допомогою блоку Given – Find точність TOL не відіграє суттєвого значення, тому її можна і не задавати.

Ще однією важливою особливістю можливостей блоку Given – Find є те, що проміжки можливих варіантів розв’язків можна вказувати і у вигляді нерівностей.

Приклад: Розв’язати систему рівнянь за умови, що Х лежить в межах від –10 до 10.

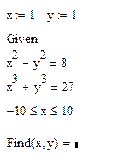
Розв’язання нерівностей.

Для аналітичного розв’язання нерівностей MathCad використовує той самий оператор Solve (розв’язати) панелі Symbolic, що і для розв’язання рівнянь. В правому маркері прописуємо нерівність, в лівому – змінну, відносно якої відбудеться розв’язання. Знаки порівняння вводимо з панелі Boolean.

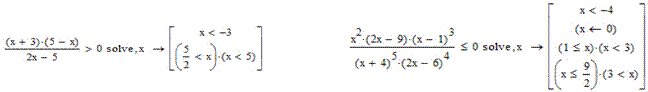Розглянемо декілька прикладів, з використанням оператора Solve, з якими MathCad працює найкраще:

Відповідь запишемо у стандартному вигляді: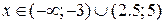

Відповідь стандартного вигляду: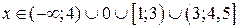

Як помітно з розглянутих прикладів, MathCad подає відповідь у дещо іншому вигляді, ніж ми звикли. Тому, для правильної інтерпретації відповіді слід пам’ятати такі правила:

1. Розв’язок оператор Solveподає у вигляді вектора, який містить елементарні нерівності. Починаючи від найменшого значення зверху до найбільшого внизу.

2. Остаточним результатом буде об’єднання всіх областей поданих у відповіді в один проміжок.

3. У кожному рядочку вектора розв’язку записаний проміжок:

- Якщо проміжок значень, яких набуває змінна, має конкретно означені числові межі (a,b), то нерівність записується у вигляді: (a<x)*(x<b). Це означає, що ч лежить в межах від a до b.

- Якщо область значень, яких набуває змінна відкрита: (x<a) або (x>a), то її другою межею буде 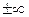. (Пр2)

- Якщо у розв’язок входить окрема точка b, то MathCad використовує позначення: 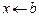. (Пр2)

- Якщо нерівність виконується при будь-яких значеннях аргументу, то в якості відповіді програма вертає сам аргумент. Наприклад:

- Якщо нерівність немає розв’язків, то MathCad видасть повідомлення: "No Solution was found". (Розв’язків немає).

4. Слід уважно слідкувати за тим, є нерівність строгою чи не строгою, так як це безпосередньо відображається в дужках, які ми використовуємо для запису проміжків у відповіді.

Зауваження: Повністю довіряти символьному процесору MathCad можна, лише при розв’язанні дуже простих нерівностей. Тому бажано уважніше ставитися до розв’язання, перевіряючи його побудовою графіка. У багатьох випадках із складними нерівностями, потрібно їх спочатку спростити.

Завдання до лабораторної роботи по даній темі

Розв’язати такі рівняння:

1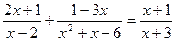

Побудувати його графік на області визначення 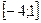Відзначити корінь на графіку.

2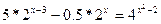

Побудувати його графік на області визначення 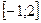Відзначити корінь на графіку.

3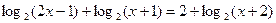

Побудувати його графік на області визначення 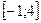Відзначити корінь на графіку.

Розв’язати системи рівнянь методом Гаусса:

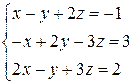
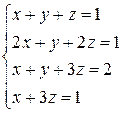
Розв’язати системи рівнянь методом Крамера:

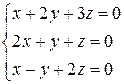
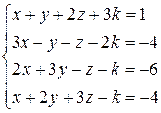
Розв’язати нерівності. Перевірити графічно правильність розв’язку.