Тема: MathCad. Спрощення виразів та алгебраїчні перетворення. Знаходження похідної та обчислення інтегралів похідних.

План

1. Розкладення виразів.
2. Розкладення на множники та зведення до спільного знаменника.
3. Винесення спільного множника за дужки.
4. Розкладення на елементарні дроби.
5. Виконання підстановки та заміни змінних.
6. Комплексне спрощення виразів.
7. Знаходження похідної першого порядку
8. Знаходження похідних вищих порядків.
9. Знаходження похідної від функції декількох змінних.
10. Знаходження інтегралів.
11. Знаходження невизначеного інтегралу.
12. Аналітичне знаходження визначеного інтегралу.
13. Знаходження кратних інтегралів.

1. Розкладення виразів.

Під розкладенням виразу розуміють математичне перетворення, яке переводить степені і добутки у більш прості для аналізу суми. У випадку розкладення тригонометричних виразів, функціі кратного аргументу перетворюються у відповідні їм функції від одинарного аргументу. Для розкладення логарифмічних функцій, використовуються відповідні формули логарифмічних спрощень.

Для проведення розкладу в MahCad існує спеціальний оператор Expand (Розкласти) панелі Symbolic (Символьні). В лівий маркер даного оператора заноситься вираз, який ми плануємо розкласти, а в правий – змінна або вираз, відносно якої відбувається розклад. Якщо вираз треба спростити максимально – правий маркер можна просто видалити, і система виконає розкладення по максимуму. Якщо спрощення потрібно провести лише до певного моменту, не до кінця, - потрібно в правому маркеру вказати ту частину виразу, яка повинна лишитися незмінною. Також можна спочатку ввести вираз, який потрібно розкласти, а потім ввести оператор Expand. Приклади розкладення різних типів виразів:

1. Розкладення алгебраїчного виразу.

Система перемножує вираз в чисельнику, зводить чисельник до спільного знаменника. Розкриває степінь в знаменнику, після чого чисельник ділиться на знаменник.

- Розглянемо різницю в результаті при заповненні правого маркера Expand, куди введемо (х):

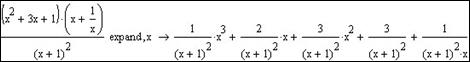у випадку розкладення дробів, заповнений правий маркер означає, що кожний елемент чисельника буде розділений на знаменник.

1. Розкладення тригонометричного виразу.

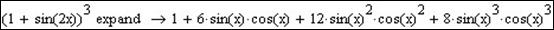
- Розглянемо різницю в результаті при заповненні правого маркера Expand, куди введемо (2х):

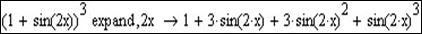
3. Розкладення тригонометричного виразу.

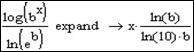Зверніть увагу на те, що десятковий логарифм представляється через відношення натуральних логарифмів.

У випадку роботи з логарифмами, використання оператора Expand є не завжди зручним, тому, що регенеруються лише натуральні логарифми за формулою 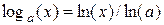. Обійти цей недолік системи – неможливо. Слід просто замінювати відношення натуральних логарифмів на логарифми з потрібною основою за даною формулою.

Крім свого прямого призначення, оператор Expand можна використовувати в якості довідника математичних формул по символьній алгебрі (особливо тригонометрії). Наприклад:

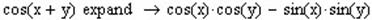
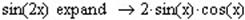
1. Розкладення на множники та зведення до спільного знаменника.

Для проведення розкладу на множники в MahCad існує спеціальний оператор Factor (від factoring – розкласти на множники)панелі Symbolic (Символьні). За допомогою оператора Factor не можна перетворити логарифмічний або тригонометричний вираз. Розкласти на множники можна тільки не дуже складний алгебраїчний вираз.

Оператор Factor має таке ж саме задання як і оператор Expand. Різниця в тому, що правий маркер потрібно обов’язково видалити, інакше результат не буде отримано.

Розкладення на множники не працює з комплексними числами. Можна розкласти лише на дійсні множники. Можливий розклад і в тому випадку, коли у вираз входять спеціальні функції, наприклад тригонометричні, коли система може використати до них звичайні алгебраїчні правила розкладу на множники.

1. Приклади розкладання на множники:

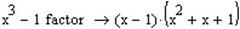
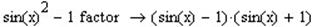
Другою важливою операцією яку виконує оператор Factor є розклад цілих чисел на прості множники.

2. Приклад розкладання чисел: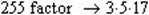

Ще однією важливою операцією, яку виконує Factor є перетворення десяткових дробів в прості дроби.

3. Приклад переведення дробів:

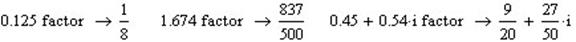
Оператор Factor використовується також для зведення до спільного знаменника. При чому в чисельник і знаменник дробів можуть входити будь-які функції та їх поєднання.

4. Приклад зведення дробів до спільного знаменника.

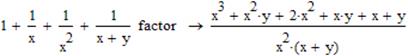
1. Винесення спільного множника за дужки.

Винесення спільного множника за дужки виконує оператор Collect (Збирати) панелі Symbolic (Символьні). Вводиться так само, як попередні оператори. В маркері зліва вказуємо вираз, з якого будемо виносити спільний множник, справа – ім’я змінної або функції, по якій проводимо дане перетворення. Винесення спільного множника може бути здійснене лише по одній змінній. Якщо доданки потрібно розподілити по декільком групам, то вираз потрібно буде ділити на частини і оперувати з кожною з них окремо.

Зазвичай, оператор Collect об’єднує в одну групу члени, в яких змінна, по якій здійснюється перетворення, входить в однаковому степені. В оператор Collect неможливо вказати вираз, який ви хочете винести за дужки. Тому він використовується лише для елементарних спрощень.

Приклад винесення спільного множника за дужки:

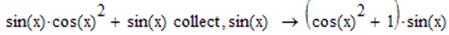
1. Розкладення на елементарні дроби.

Для розкладення виразу на елементарні дроби в MathCad використовують оператор Parfrac (елементарні дроби) панелі Symbolic. В лівому маркері оператора прописуємо вираз, який потребує спрощення, в правому – змінна, виходячи з якої повинно бути проведено спрощення. В якості змінних можуть бути використані функції.

Приклад розкладу на елементарні дроби:

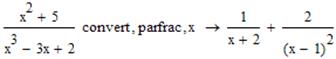
1. Виконання підстановки та заміни змінних.

Для виконання підстановки в MathCad використовують оператор Substitute (Замістити) панелі Symbolic (Символьні).

Вводиться оператор так само, як і попередні оператори. В правому маркері робимо запис: a=b, де b – вираз або значення, яке ми підставляємо на місце змінної a. Якщо потрібно замінити дві змінні, то через кому робимо ще одне аналогічне присвоєння. Але замість звичайного дорівнює ставимо дорівнює з панелі Boolean (Булеві). Оператор Substitute працює як із змінними, так і з функціями. ( 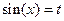). Слід зауважити, що система погано працює з коренями.

Приклад підстановки:

1. Комплексне спрощення виразів.

Спрощення, для здійснення якого потрібно виконати декілька операцій різного роду, будемо називати комплексним спрощенням.

В простих випадках аналітичний процесор MathCad здатний проводити комплексне спрощення самостійно. Для цього служить спеціальний символьний оператор Simplify (Спростити),панелі Symbolic. Можливості оператора Simplify суміщають в собі можливості вивчених попередньо операторів. Крім того, оператор Simplify може зводити подібні доданки, та виконувати арифметичні обрахунки, суміщає всі виконані операції таким чином, щоб спрощення було максимальним.

Простий приклад:

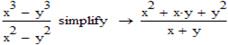
За умовчанням MathCad сприймає всі змінні як комплексні числа, тому у випадках, коли спрощення залежить від того, які значення може приймати змінна (вирази з коренем, логарифмічні вирази), потрібно наперед обумовити можливі значення або параметри змінної.

Для цього в MathCad є спеціальний оператор Modifier (Модифікація) панелі Symbolic. Він відкривається у вигляді окремої панелі, що складається з чотирьох операторів. ((Відкрили, подивилися)). Вводити їх можна як з панелі так і з клавіатури. Розглянемо кожен з них:

- Assume(Прийняти) слово – заготовка для створення оператора модифікації.

- Real(Дійсне) описує змінну як дійсне число.

- RealRange (a,b) (Дійсна область) дозволяє обмежити область визначення змінної або константи відрізком між дійсними числами a і b.

- Trig (Тригонометричні) розглядає змінну як тригонометричну величину. На практиці використовується рідко, так як реально практично ні на що не впливає.

НайкращеMathCad спрощує арифметичні та логарифмічні вирази. Погано працює з коренями та тригонометричними функціями. Якщо вам потрібно спростити складний вираз, потрібно скеровувати програму в потрібному напрямку. Розглянемо Приклад 1:

Спростити вираз:

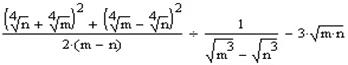
Оперувати таким великим виразом досить непросто. Тому розділимо його на три частини і будемо проводити спрощення поетапно. В першу чергу будемо розкривати квадрати в чисельнику першої частини виразу.

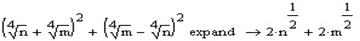
ОператорSimplify погано працює з коренями та дробовими степенями то ми надалі виконаємо заміну (m=x², n=y²), накладемо проміжок значень змінної (x≥0, y≥0), та спростимо (Simplify).

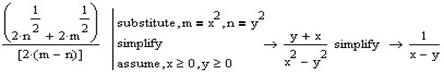
Виконаємо заміну в другій частині виразу:

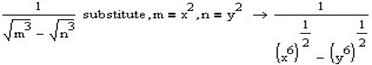
Спростимо її разом із першою частиною, яку ми спростили попередньо:

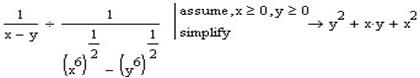
Виконаємо заміну в третій частині виразу :

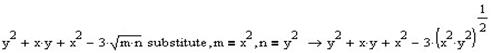
Та спростимо її разом з попередньою:

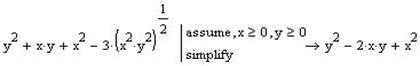
Розкладаємо отриманий вираз на множники та виконуємо зворотню заміну:

.

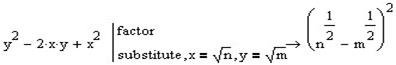Приклад 2:

Спростити тригонометричний вираз таким чином, щоб в результаті отримати добуток тригонометричних функцій:

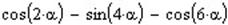
Для початку потрібно звести функції, що входять до даного виразу до функцій з однаковим аргументом (2α). Для цього використаємо оператор Simplify.

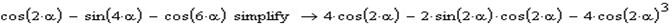
Наступним етапом буде розкладення на множники:

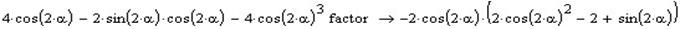
Виконаємо спрощення виразу в дужках. Для цього потрібно замінити косинус на синус, а потім розкласти на множники.

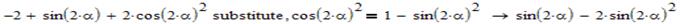
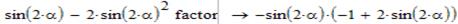
Суміщаємо першу частину, яку ми лишили – ((-2*cos(2α))) з другою, яку ми щойно спростили. Виконаємо загальне спрощення:

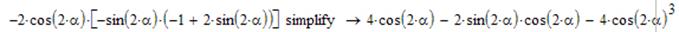
Знаємо, що 2sin2α*cos2α=sin4α, виконаємо заміну:

І виконаємо подальше розв’язання:

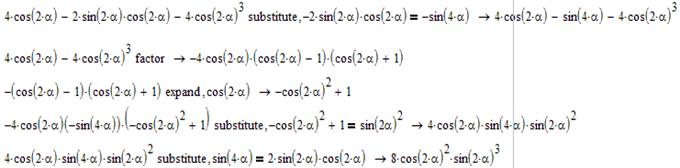
Звернемо увагу на те, що процес спрощення відбувається громіздко і важко. Простіше розв’язати особисто на папері. Те, що ми з вами повинні вивчити – ми розібрали. Вибір – користуватися спрощенням в MathCad чи ні – за вами.

Знаходження похідних.

Аналогічно до інших найбільш важливих математичних операцій, в Mathcad передбачено чисельне і символьне диференціювання. Практично в 99% випадків можна знайти аналітичне значення похідної. Чисельне знаходження похідних потрібне лише для ряду специфічних задач. Також слід зауважити, що чисельне диференціювання при великих степенях дає велику похибку.

Для операцій диференціювання та інтегрування ми будемо користуватися панеллю Calculus (Обчислення) Математичної панелі.

7. Знаходження похідної першого порядку.

Для знаходження похідної першого порядку в Mathcad використовують оператор Derivative з панелі Calculus. Оператор Derivativeмає два маркера, принцип заповнення їх відповідає математичним стандартам: в верхній вводимо функцію, в нижній – змінну, по якій відбувається диференціювання.

Якщо вираз, який ми диференціюємо складається з добутків, або різниць, його треба взяти в дужки. В якості оператора виводу результату використовуємо або → або = в залежності від того, символьний чи чисельний результат нам потрібен.

При символьному диференціюванні можна оперувати функціями декількох змінних та функціями з параметрами. Також оператор диференціювання може можна поєднувати із будь-яким іншим обчислювальним або символьним оператором.

Розглянемо приклад:

З прикладу1 видно, що знайдено похідну лише від першої частини виразу.

З прикладу2 видно, що знайдено похідну 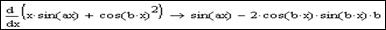від усього виразу, що в дужках.

Також можна знайти похідну, спочатку задавши функцію, а потім ввівши її ім’я у відповідні маркери диференціювання.

8. Знаходження похідних вищих порядків.

Для знаходження похідних вищих порядків використовують оператор Nth Derivative панелі Calculus. Оператор має в собі чотири маркера. Вони заповнюються повністю у відповідності до правил прийнятих в математиці. Достатньо ввести показник степеня в один з маркерів, як він відобразиться в другому автоматично.

Порядок похідної обов’язково повинен бути числом. Аналітичне знаходження похідної з неявно заданим порядком – неможливий. А ось функція, від якої ми знаходимо похідну, може бути як завгодно складною. Також функція може містити в собі параметри.

Приклад:

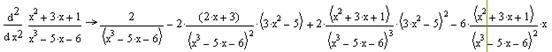
Із приклада видно, що символьний процесор шукаючи похідну не спрощує вираз. Тому, для того, щоб отримати відповідь у спрощеному вигляді, потрібно застосувати оператор Simplify.

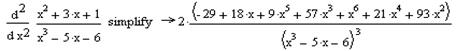
Аналогічно звичайним похідним, похідні вищих порядків також можна знаходити як аналітично так і чисельно. Однак, слід зауважити, що при чисельному знаходженні, порядок похідної не може бути вище ніж 5. (При спробі задання вищого порядку ніж 5, програма видасть повідомлення про помилку). Це пов’язано з тим, що при застосуванні чисельного метода накопичується велика похибка. Тому в таких випадках завжди варто використовувати символьний процесор.

9. Знаходження похідної від функції декількох змінних.

Для того, щоб знайти похідну від функції декількох змінних (Частинну похідну), потрібно спочатку перетворити оператор Derivative.Для цього:

- вводимо оператор Derivative.

- Викликаємо на ньому контекстне меню.

- Вибираємо пункт: - View Derivative as (зобразити похідну як).

- Вибираємо пункт Partial Derivative. (частинна похідна)

Якщо буде потрібно повернутися до звичайного вигляду оператора, дії виконати послідовно навпаки. Так само можна обчислювати похідні декількох функцій вищих порядків.

Приклад: Знайти всі частинні похідні для функції f(x,y,z)=x²*e^x+z-y³

Розв’язання:

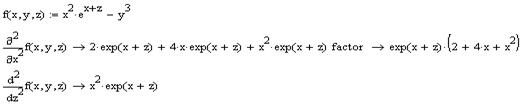
10. Знаходження інтегралів.

Знаходження визначених інтегралів в Mathcad може бути як чисельним так і символьним. Обчислення невизначених – тільки символьним. У будь-якому випадку, спочатку потрібно намагатися отримати аналітичний результат, я лише у випадку невдачі – чисельний.

Також в Mathcad можна обчислювати подвійні, потрійні а також невласні інтеграли.

На практиці 99% задач на знаходження інтегралів розв’язується правильно. У яких випадках програма не може виконати завдання:

- Якщо функція, у тому вигляді, в якому ви її задали, не підпадає під жодну формулу інтегрування, що міститься в довіднику програми. У цьому випадку потрібно виконати певну заміну або спрощення перед інтегруванням.

- Якщо результат є надто великим, не піддається спрощенню і його неможливо вивести не екран. У цьому випадку потрібно розбити початкову функцію на декілька частин і брати інтеграл від кожної з них.

- Якщо функція, яку потрібно про інтегрувати, містить в собі рекурентні співвідношення, ряди та їх добутки.

11. Знаходження невизначеного інтегралу.

Для знаходження невизначеного інтегралу в Mathcad існує спеціальний оператор Indefinite Integral (Невизначений інтеграл) панелі Calculus (Обчислювальні). Його зображення на кнопці цілком відповідає зображенню, прийнятому в математиці. Оператор невизначеного інтеграла має два маркера. Заповнюємо їх відповідно до правил математики: в лівий маркер вводимо функцію, в правий – змінну, по якій проводимо інтегрування. В кінці ставимо оператор символьного виводу "→".

Приклад: Знайти невизначений інтеграл.

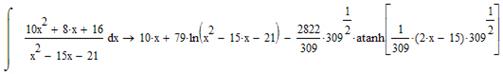
Часто буває, що результат інтегрування виявляється занадто громіздким і його бажано було б спростити. Для цього використовують оператори панелі Символьні: Simplify для простого спрощення, Collect – для зведення подібних доданків, Expand – для розкладення степенів та Factor – для приведення до спільного знаменника. Для того, щоб задіяти потрібний символьний оператор, потрібно виділити вираз інтеграла і натиснути відповідну кнопку панелі Symbolic. Для спрощення результату інтегрування можна застосовувати одразу по кілька операторів.

Слід зауважити, що в кінцевій відповіді Mathcad не додає константу С. Тому, якщо це є важливим, в оформленні потрібно дописати +С самостійно.

1. Аналітичне знаходження визначеного інтегралу.

Для знаходження визначеного інтегралу в Mathcad існує оператор Definite Integral (Визначений інтеграл) панелі Calculus. Оператор Definite Integral має вигляд такий самий як і в математиці, містить в собі чотири маркера, які заповнюються відповідно правилам інтегрування. Знаходити чисельний результат варто лише в тому випадку, коли неможливо знайти аналітичний. Якщо відповідь вийде надто громіздкою, слід користуватися операторами, що використовуються для спрощення.

Приклад1 стандартний і приклад2 для знаходження інтегралу з неявно заданими межами:

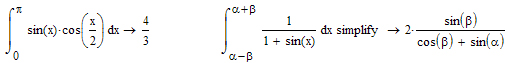
У випадку знаходження інтегралів з неявно заданими межами слід використовувати оператор Simplify для отримання простого варіанту відповіді. Також слід пам’ятати, що всі функції і числа Mathcad розглядає в комплексній області, тому неправильно задавши межі можна отримати комплексне значення. Якщо потрібно отримати результат інтегрування у вигляді числа, достатньо поставити знак "=" після аналітичної відповіді, або застосувати оператор Float із потрібною точністю.

1. Знаходження кратних інтегралів.

Для того, щоб знайти кратний інтеграл потрібно виконати таку послідовність дій:

1. Ввести з панелі Calculusпотрібний вам оператор інтегрування.
2. Поставити курсор в маркер підінтегральної функції і ввести другий оператор інтегрування. Для обчислення потрійного інтеграла, потрібно виконати цю операцію два рази.
3. В маркері останнього з заданих операторів прописати функцію, яку потрібно проінтегрувати.
4. Заповнити маркери диференціалів у тому порядку, в якому повинно відбуватися інтегрування.
5. Якщо знаходиться визначений інтеграл – заповнюємо маркери відповідних меж.

Приклад: Обчислити значення кратного інтегралу:

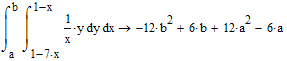
Слід пам’ятати, що і у випадку знаходження кратних інтегралів, чисельний метод застосовується лише тоді, коли символьний процесор не може виконати завдання.