Лекція 3. Тема: Mathcad. Матричні обчислення.

План:

1. Створення матриць та векторів. Робота з даними.
2. Елементарні матричні обчислення.
3. Вектори. Дії над векторами.
4. Використання матричних функцій.

1. Створення матриць та векторів. Робота з даними.

Панель Matrix (Матричні).

До операторів панелі Matrix (Матричні) відносяться:

Matrix or Vector (Матриця або вектор) – Додає матрицю або вектор.

Subscript (Індекс) – Використовується для задання індексу певного елемента матриці.

Inverse (Обернений). Оператор знаходження оберненої матриці.

Determinant (Визначник). Для знаходження визначника матриці або модуля вектора.

Vectorize (Векторизація). Пропонує у визначеному виразі робити операції поелементно.

Matrix Column (Стовпець матриці). Використовується для виділення стовпця матриці.

Matrix Transpose (Матричне транспонування). Використовується для виділення рядка або транспонування матриці.

Range Variable (Ранжовані змінні) Використовується як аналог програмних операторів циклу.

Dot Product (Множення). Використовується для множення матриць.

Cross Product (Векторний добуток). Використовується для знаходження добутку векторів.

Vector Sum (Сума). Підсумовує елементи вектора. Повертає скаляр.

Picture (Зображення). Дозволяє вставку зображень в документ.

Найбільш простим способом задання матриці є використання спеціальної панелі Insert Matrix (Вставити матрицю) робочої панелі Matrix (Матричні). Параметри матриці задаємо у віконечках Rows (рядки) і Columns (колонки). Тобто, якщо потрібно ввести матрицю, розмірністю 2×2, то ставимо 2 там, де рядки, і 2 там де стовпчики. ((Відкрили і подивилися)). Якщо потрібно задати вектор, то у віконечку Columns (колонки) ставимо 1. Елементи матриці можна представляти у вигляді літер, цифр та виразів. На практиці зазвичай оперують не матрицями, а їх іменами. Для цього треба присвоїти значення матриці певній змінній. Для цього спочатку вводимо змінну, потім оператор присвоєння, потім вводимо саму матрицю. Якщо серед символів та виразів, які є елементами матриці є невідомі або параметри, то слід обов’язково обумовити їх перед заданням матриці. Якщо елементами матриці є текст, то його потрібно взяти в лапки.

Приклад1: Задання матриць з елементами-змінними та елементами-функціями.

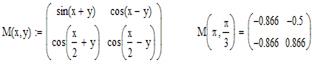
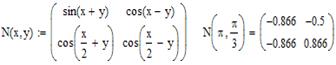
В заданій матриці завжди можна отримати значення будь-якого її елемента, використовуючи матричні індекси (а_1,2- другий елемент першого рядка). В нашій математиці відлік рядків і стовпців прийнято починати з 1. Але слід пам’ятати, що в програмуванні початкові індекси дорівнюють 0. Щоб змінити початковий індекс: Tools→ Worksheets Options→ Built-in Variables→ ORIGIN (1). Можна зробити інакше. На початку обрахувань в документі присвоїти ORIGIN:=1.

Для того, щоб отримати значення певного визначеного матричного елемента потрібно ввести ім’я матриці із відповідним індексом. Для цього використовуємо оператор Subscript (Індекс) панелі Matrix. На першому місці індексу ставимо номер рядка, на другому – стовпця через кому. При визначенні елемента вектора вказуємо тільки номер рядка.

Приклад2: Винесення елементів матриці.

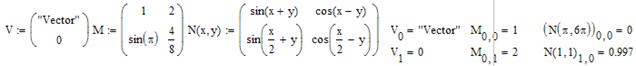
Можна виносити не тільки окремі елементи, а і цілі рядки або стовпці матриці. Для цього використовують такі оператори панелі Matrix, як Matrix Column (Стовпець матриці) – виносить стовпець матриці та Matrix Transpose (Матричне транспонування) – виносить рядок матриці.

Приклад3: Винесення з матриці рядків та стовпців.

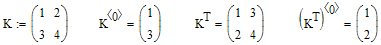
1. Елементарні матричні обчислення.

Всі простіші операції матричної алгебри реалізовані в системі Mathcad за допомогою операторів. Вид кожного з них повністю відповідає прийнятим в математиці позначенням. Але слід зауважити: Всі оператори векторних перетворень в Mathcad працюють тільки у випадку матриць-стовпців. Тому вектори, що представлені матрицею-рядком, потрібно спочатку транспонувати.

Додавання та віднімання матриць.

Для того, щоб додати чи відняти матриці використовують звичні символи «+», «--». Дії виконуються за математичним правилом додавання та віднімання матриць. Також при додаванні чи відніманні матриць можна використовувати коефіцієнти.

Приклад4: Додавання та віднімання матриць. Дано матриці А і В. Знайти матрицю А+В та матрицю Х, що задовольняє умові 3А-2Х=В

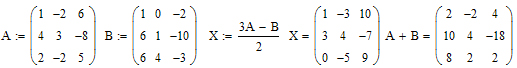
Множення матриць.

Множення матриць в Mathcad відбувається у відповідності до правил лінійної алгебри, що стосуються матриць (правило множення рядка на стовпець). Пам’ятаємо, що перед тим, як множити матриці, потрібно перевірити, чи вони є узгодженими.

Для множення матриць в Mathcad використовується простий знак «*», введений з клавіатури, або ж оператор Dot Product (Множення), введений з панелі Matrix. Перемножувати матриці можна у тому випадку, коли елементами її є числа, тоді ми використовуємо знак чисельного обчислення; і тоді, коли елементами матриці є символи або вирази. В цьому випадку для виводу результату ми використовуємо оператор аналітичного числення.

Якщо ви спробуєте перемножити матриці, що не є узгодженими – система видасть вам повідомлення про помилку.

Приклад5: Матричне множення.

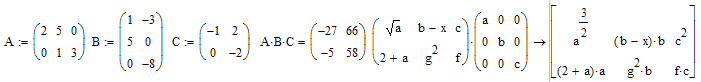
Транспонування матриць.

Оператор транспонування Matrix Transpose знаходиться на панелі Matrix. Також його можна ввести з меню або панелі Symbolic. Транспонування виконується згідно правил лінійної алгебри. Виконується для матриць як із числовими так і з символьними елементами.

Визначник матриці.

Оператор знаходження визначника матриці Determinant (Визначник) знаходиться також на панелі Matrix. Його вигляд відповідає прийнятому в математиці. Обчислювати визначник можна чисельно і символьно.

Обернена матриця.

Знаходження оберненої матриці – одна з основних задач матричної алгебри, оскільки вона постійно використовується у розв’язаннях та доведеннях. Оператор знаходження оберненої матриці Inverse (Обернений) знаходиться на панелі Matrix. Для матриць з елементами-символами задіюємо оператор визначення оберненої матриці, що знаходиться на панелі Symbolic.

Приклад6: Знаходження оберненої матриці.

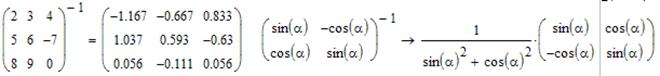
Також в Mathcad можна підносити матриці у степінь. Для цього використовується кнопка піднесення до степеня панелі Калькулятор.

1. Вектори. Дії над векторами.

Модуль вектора.

Для визначення модуля вектора використовуємо оператор Determinant (Визначник) панелі Matrix.

Приклад7: Задача на знаходження векторів та їх модулів.

Задача: Точки А(11,-9,7), В(9,6,0), С(-5,15,-1) є послідовними вершинами ромба. Знайти координати четвертої вершини D, довжини діагоналей ромба, його периметр.

Розв’язання:

Складемо математичний алгоритм розв’язку:

1. Що потрібно зробити, щоб знайти координати т.D? Знайти вектори ВА і ВС. Потім, додавши ВА і ВС за правилом паралелограма – отримаємо вектор ВD. Знаючи координати його початку зможемо знайти координати кінця - т.D.

Тепер правильно оформлюємо розв’язання в програмі. Задаємо координати вершин в векторній формі: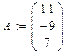

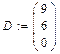
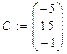
Знаходимо вектори ВА і ВС:

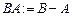
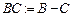
Знаходимо ВD:

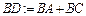
Знаходимо т. D :

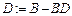
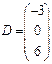
1. Знайдемо довжини діагоналей. Для цього будемо знаходити модулі векторів ВD і АС.

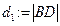
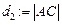
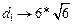
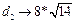
1. Знаходимо периметр. Беремо довжину сторони. Множимо її на 4, адже всі сторони рівні, і отримуємо те, що було потрібно.

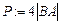
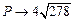
Відповідь: (записуємо в текстову область) D(-3,0,6); d1=6 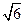; d2=8 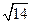; Р=4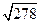

Векторний добуток.

Позначається векторний добуток в Mathcad символом «×». Ввести його можна за допомогою оператора Cross Product панелі Matrix.

Скалярний добуток.

Для того, щоб в Mathcad помножити скалярно два вектори потрібно або скористатися оператором Dot Product (множення) панелі Matrix, або просто ввести символ «*» з клавіатури.

4. Використання матричних функцій.

Існує ряд матриць спеціального виду (верхні і нижні трикутні, одиничні, скалярні, нульові і т д). В Mathcad є декілька функцій, які дозволяють швидко і просто задавати матриці такого типу. Для того, щоб ввести таку функцію достатньо просто набрати її з клавіатури або через меню Insert→ Function→ знайти в Function Category розділ Vector and Matrix і обрати відповідно потрібну вам функцію.

Функції задання матриць спеціального виду:

1. identity (N). Дана функція служить для задання одиничної матриці матриці розмірності N.

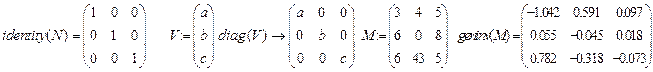
1. diag (V). Функція створює матрицю, елементи головної діагоналі якої рівні відповідним елементам вектора V.
2. geninv (M). Функція знаходження оберненої матриці. Її використання аналогічно оператору M^-1 панелі Matrix.
3. augment (A,B…), де А, В – матриці. Функція служить для злиття матриць зліва направо. Відповідно правилу, матриці, що з’єднуються повинні мати однакову кількість рядків.
4. stack (A,B…), де А, В – матриці. Функція відповідає за злиття матриць зверху вниз. У цьому випадку матриці повинні мати однакову кількість стовпців.

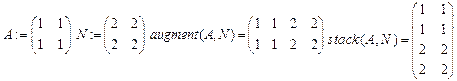
1. rank (M). Функція служить для знаходження рангу матриці.

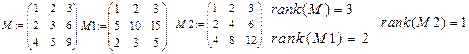
Завдання на лабораторну роботу по даній темі.

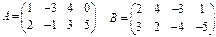1. Знайти А+В, А-В, якщо:

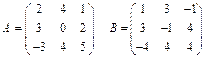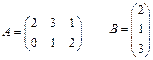2. Знайти АВ, якщо:

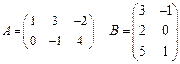3. Знайти АВ і ВА, якщо:

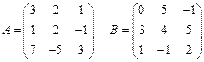
4. Знайти матрицю АВ – 2ВА + 3Е, якщо:

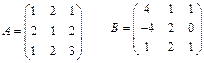
5. Знайти матрицю, обернену до А:

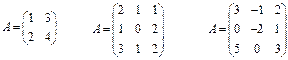
6. Знайти матрицю А^-1 – В, якщо:

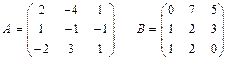
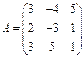
7. Знайти матрицю 6А + А^-1, якщо:

8. Точки А(4;1), В(3;5), С(-1;4), D(0;0) є вершинами квадрата. Знайти площу квадрата, довжину його сторони, та координати середин сторін.

9. Дано вектори 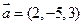, 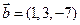. Знайти вектори ,

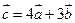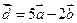
10. Знайти периметр трикутника ABC, з вершинами A(8,0,7), B(10,2,8), C(10,-2,8).

Приклади на використання матричних функцій:

1. Створити одиничну матрицю розмірністю k=7.

2. Дано вектор 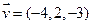. Створити діагональну матрицю з елементами вектора .

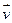3. Дано матрицю L. За допомогою матричних функцій знайдіть обернену до неї матрицю.

4. Дано матриці S, T. Виконати їх злиття зліва на право та зверху вниз.

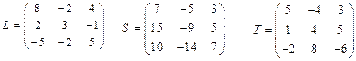5. Знайти ранг матриць L, S, T.