Абсолютно непружне зіткнення кулі та маятника. Енергія дисипації

Відразу після абсолютно непружного зіткнення циліндр 2 із кришкою 3 разом із кулею рухаються зі швидкістю 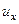як одне ціле. Потім вони піднімаються вгору на висоту h (рис. 2.4.1), де їх швидкість стає такою, що дорівнює нулю. Кінетична енергія маятника і кулі, яку вони отримали відразу після зіткнення, переходить у потенціальну енергію у полі сили тяжіння:

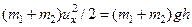. (2.4.6)

Тут і далі індексом „1” позначено відповідні характеристики кулі, індексом „2” – відповідні характеристики балістичного маятника (циліндр 2 із кришкою 3, рис. 2.4.1).

Висоту 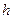неважко знайти із прямокутного трикутника ABC (рис. 2.4.1):

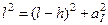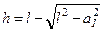; , (2.4.7)

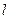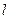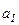де – довжина нитки ( =АС), – переміщення маятника, яке вимірюється лінійкою 1 (індекс „ I ” вказує, що вимір проводиться для випадку абсолютно непружного зіткнення).

Експериментально знайшовши переміщення 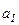та застосовуючи формули (2.4.7) та (2.4.8), можна легко знайти швидкість маятника та кулі після удару:

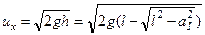. (2.4.8)

Швидкість кулі перед ударом знайдемо, виходячи із закону збереження імпульсу (2.4.2):

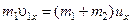. (2.4.9)

Тут враховано, що швидкість маятника перед зіткненням дорівнює нулю, маси кулі та маятника вважаємо відомими. Далі з (2.4.8) та (2.4.9) отримуємо

.
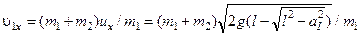(2.4.20)

Тепер неважко знайти енергію дисипації, виходячи із співвідношень (2.4.8), (2.4.20) та (2.4.5):

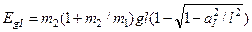. (2.4.21)