Опис експериментальної установки та методу дослідження. Обертання твердого тіла навколо нерухомої осі OZ описується рівнянням

Обертання твердого тіла навколо нерухомої осі OZ описується рівнянням

, (2.3.1)

де 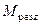– проекція на вісь обертання результуючого моменту сил, 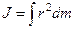– момент інерції тіла відносно осі OZ, 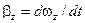– проекція на вісь OZ кутового прискорення тіла.

Рівняння (2.3.1) є прямим наслідком другого закону Ньютона. Тому його експериментальна перевірка є водночас перевіркою основних положень механіки.

Експериментальна установка, схема якої зображена на рис. 2.3.1 (маятник Обербека), складається із чотирьох спиць 1, закріплених на втулці під прямим кутом одна до одної. На цю саму втулку насаджено шків 2, радіус якого дорівнює 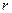.Уся система може вільно обертатися навколо горизонтальної осі. Момент інерції системи можна змінювати, пересуваючи чотири тягарці Б (позиція 3, рис. 2.3.1) уздовж кожної із чотирьох спиць 1.

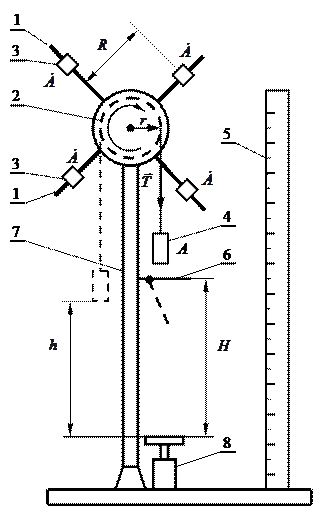
Рисунок 2.3.1 – Схема експериментальної установки: 1– спиці маятника; 2 – шків маятника; 3 – тягарці Б масою m₀; 4 – тіло А з масою m_А; 5 – лінійка; 6 – верхній столик-вимикач; 7 – вертикальна опора; 8 – нижній столик-вимикач

На шків 2 намотана нитка, до якої прив’язаний тягарець А масою m_А (позиція 4, рис. 2.3.1). Сила тяжіння, що діє на цей тягарець, приводить до появи сили натягу нитки, а це, у свою чергу, спричиняє обертання маятника Обербека.

Для маятника Обербека неважко експериментально знайти результуючий момент сил, момент інерції, кутове прискорення, а потім перевірити справедливість рівняння (2.3.1). Знайдемо співвідношення, за допомогою яких, використовуючи експериментальні дані, можна обчислити вищезгадані величини.

Виміряємо час t, за який тіло А (позиція 4, рис. 2.3.1) зі стану спокою опуститься на відстань H (рис. 2.3.1). Рух тіла А є рівноприскореним. Це прискорення легко знайти з формули

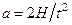. (2.3.2)

Кутове ж прискорення знаходимо, використовуючи відоме співвідношення

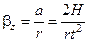. (2.3.3)

У цій формулі r – радіус шківа.

Результуючий момент сил, що діє на маятник Обербека, складається з моменту сили натягу нитки та моменту тертя в осі втулки:

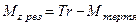, (2.3.4)

де 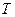– сила натягу нитки.

Силу натягу нитки знаходимо за допомогою другого закону Ньютона, який застосовуємо до руху тіла А:

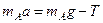. (2.3.5)

Для знаходження моменту сили тертя використаємо закон збереження енергії. Тіло А опускається на відстань H, яка визначається довжиною нитки, що прив’язана до шківа. Після досягнення тілом А найнижчої точки (відстань H) маятник продовжує обертатися за інерцією в тому самому напрямку і намотує нитку на шків. Тіло А починає підніматись і зупиняється на висоті h (рис. 2.3.1). Завдяки силі тертя висота підняття h виявляється меншою за відстань H. Експериментально вимірявши величини h та H, можна знайти момент сил тертя. Для цього використаємо те, що робота сил тертя дорівнює зміні повної енергії системи. Тобто

,
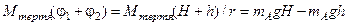(2.3.6)

де 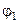– кут повороту маятника за час спуску тіла А на відстань H; 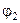– кут повороту маятника за час підйому тіла А на висоту h. Використовуючи формули (2.3.2), (2.3.4) – (2.3.6), знаходимо результуючий момент сил, що діє на маятник Обербека:

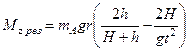. (2.3.7)

Для знаходження моменту інерції маятника використаємо

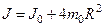, (2.3.8)

де 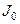– момент інерції маятника без чотирьох тягарців Б масою 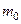; R – відстань цих тягарців до осі обертання. Зазначимо, що, використовуючи формулу (2.3.8), ми вважаємо тягарці Б (позиція 3, рис. 2.3.1) масою 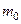точковими тілами, які знаходяться від осі обертання на однаковій відстані R.

Таким чином, формули (2.3.3), (2.3.7) та (2.3.8) дозволяють за результатами експерименту знайти всі величини, що входять до основного рівняння динаміки обертального руху (2.3.1), і тим самим перевірити його.