Частково пружне зіткнення кулі та маятника. Коефіцієнт відновлення відносної швидкості та енергія дисипації

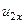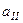Після частково пружного удару балістичний маятник рухається зі швидкість , а куля – зі швидкістю . Швидкість маятника після удару можна знайти, вимірявши переміщення маятника (індекс „ II ” свідчить про те, що вимір проводиться для випадку частково пружного зіткнення) і використавши формулу, аналогічну (2.4.8):

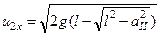. (2.4.22)

Швидкість кулі перед зіткненням визначається параметрами трубки 5 (рис. 2.4.1) і є однаковою як для випадку частково пружного удару, так і абсолютно непружного зіткнення. Ця швидкість визначається формулою (2.4.20). Щоб знайти швидкість кулі після зіткнення, застосуємо закон збереження імпульсу (2.4.2):

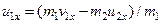. (2.4.23)

Тут використали, що швидкість маятника перед зіткненням дорівнює нулю. Таким чином, для даного експерименту нам є відомими як швидкості тіл перед зіткненням, так і після зіткнення. Використовуючи формули (2.4.20), (2.4.21), (2.4.23), а також означення (2.4.4), знаходимо коефіцієнт відновлення відносної швидкості для частково пружного удару:

або

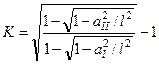. (2.4.24)

Неважко знайти й енергію дисипації для частково пружного удару, якщо використати формули (2.4.20), (2.4.21), (2.4.23) та (2.4.5):

.
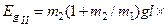
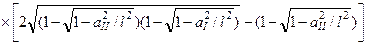(2.4.25)

Зазначимо, що з формул (2.4.24) та (2.4.25) випливає: коли коефіцієнт відновлення відносної швидкості дорівнює 1, то енергія дисипації дорівнює нулю. Дійсно, у випадку абсолютно пружного удару коефіцієнт відновлення відносної швидкості дорівнює 1, а енергія дисипації дорівнює нулю.