Опис експериментальної установки та методу дослідження. У лабораторній роботі необхідно експериментально знайти відношення теплоємності при сталому тискові до теплоємності при сталому об'ємі для повітря
У лабораторній роботі необхідно експериментально знайти відношення теплоємності при сталому тискові 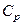 до теплоємності при сталому об'ємі
до теплоємності при сталому об'ємі 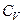 для повітря
для повітря
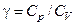 . (3.1.1)
. (3.1.1)
Сталу 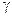 , що визначається співвідношенням (3.1.1), називають сталою адіабати. Це пов’язано з тим, що
, що визначається співвідношенням (3.1.1), називають сталою адіабати. Це пов’язано з тим, що 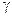 належить до рівняння, яке описує адіабатичний процес:
належить до рівняння, яке описує адіабатичний процес:
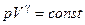 . (3.1.2)
. (3.1.2)
Рівняння (3.1.2) називається рівнянням Пуассона.
Сталу адіабати можна визначити експериментально за допомогою методу Клемана-Дезорма. Відповідно до цього методу використовуємо схему експериментальної установки, що зображена на рис. 3.1.1. Установка складається з балона 1, манометра 2, насоса 3, шкали манометра 4 та клапана 5 (рис. 3.1.1).
Сутність методу Клемана-Дезорма полягає у такому. Накачаємо в балон 1 повітря за допомогою насоса 3 (клапан 4 при цьому повинен бути закритим). Зразу ж після накачування температура повітря в балоні збільшиться, але потім через деякий час зрівняється з температурою повітря в лабораторії T 1 = T 0 . Завдяки накачуванню повітря тиск у балоні p1 буде вищим за атмосферний p0. Початковий стан повітря в балоні характеризується параметрами p1 та Т1 і зображений на діаграмі рис. 3.1.2 точкою 1.
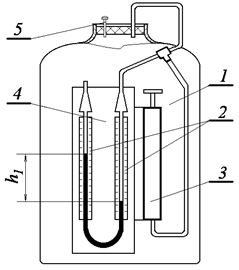
Рисунок 3.1.1 – Схема експериментальної установки: 1 – балон; 2– манометр; 3 – насос; 4 – шкала манометра; 5 – клапан
Тиск 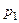 можемо виміряти експериментально за допомогою манометра:
можемо виміряти експериментально за допомогою манометра:
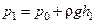 ,
, 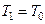 , (3.1.3)
, (3.1.3)
де r – густина рідини манометра; h1 – перепад рівнів рідини в манометрі, який знаходимо експериментально (рис. 3.1.1); 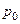 – атмосферний тиск;
– атмосферний тиск; 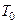 – температура повітря в лабораторії.
– температура повітря в лабораторії.
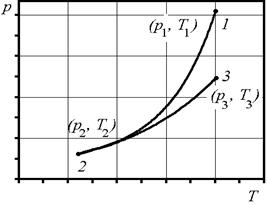
Рисунок 3.1.2 – 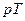 –діаграма процесів, що відбуваються в експериментальній установці
–діаграма процесів, що відбуваються в експериментальній установці
Відкриємо клапан 5 і відразу закриємо його так, щоб тиск у балоні встиг зрівнятися з атмосферним. Процес виходу повітря з балона відбувається досить швидко і його можна вважати адіабатним тому, що за цей час тіла не встигають обмінюватися теплом один з одним. Після адіабатного розширення тиск газу в балоні дорівнюватиме атмосферному, тобто p2 = p0, а температура Т2 буде нижчою за температуру T1 = T0 . Стан після адіабатичного розширення характеризується параметрами p2 та Т2 і поданий на рис. 3.1.2 точкою 2:
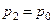 ,
, 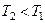 .
.
З часом температура повітря в балоні за рахунок теплообміну підвищиться і стане дорівнювати кімнатній: 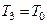 . Тиск також підвищиться до значення р3. Об'єм повітря залишиться незмінним (балон закритий). Цей стан характеризується параметрами p3 та Т3 і зображений на рис. 3.1.2 точкою 3. Тиск
. Тиск також підвищиться до значення р3. Об'єм повітря залишиться незмінним (балон закритий). Цей стан характеризується параметрами p3 та Т3 і зображений на рис. 3.1.2 точкою 3. Тиск 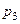 можемо виміряти експериментально за допомогою манометра:
можемо виміряти експериментально за допомогою манометра:
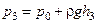 ,
, 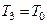 . (3.1.4)
. (3.1.4)
Опишемо вищезазначені процеси математично. Перехід газу зі стану 1 у стан 2 відбувається адіабатично. Це означає, що
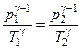 або
або 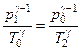 , (3.1.5)
, (3.1.5)
де використано, що 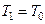 ,
, 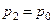 . Зі стану 2 у стан 3 газ, що залишився у балоні, переходить ізохорично:
. Зі стану 2 у стан 3 газ, що залишився у балоні, переходить ізохорично:
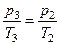 або
або 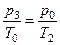 . (3.1.6)
. (3.1.6)
Виключимо з (3.1.5) і (3.1.6) температуру та отримаємо
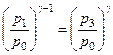 . (3.1.7)
. (3.1.7)
Підставимо в рівняння (3.1.7) співвідношення (3.1.3) та (3.1.4):
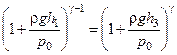 .
.
Використаємо відоме співвідношення 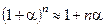 , а також умову, що
, а також умову, що 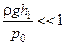 і
і 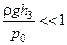 . Тоді одержимо
. Тоді одержимо
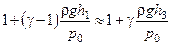 ,
,
або
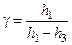 . (3.1.8)
. (3.1.8)
Вираз (3.1.8) є розрахунковою формулою лабораторної роботи. Вимірюючи h1 та h3, за допомогою (3.1.8), можна визначити шукане відношення теплоємностей 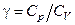 .
.
Дата добавления: 2015-05-05; просмотров: 1001;
