Абсолютно пружній удар
При якому кінетична енергія системи не міняється, в 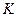 -системі описується системою рівнянь
-системі описується системою рівнянь
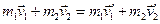
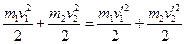 .
.
Розв’яжемо цю систему. Перепишемо рівняння у вигляді
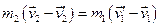 ,
,
а рівняння у вигляді
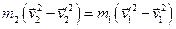 .
.
Після ділення на одержуємо
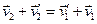 .
.
Підставимо вираз
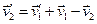
у формулу
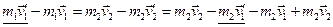
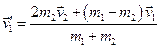 .
.
В чисельнику додамо і віднімемо 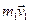
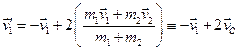 .
.
Аналогічно отримаємо
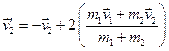 .
.
Цікаве те, що при рівності мас кульок 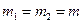 вони в результаті удару обмінюються швидкостями
вони в результаті удару обмінюються швидкостями
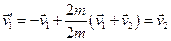 .
.
Можна розглянути рівняння і при умові 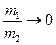 , що відповідає „нальоту частинки на стінку”. При цьому наближенні одержимо наступний розв’язок
, що відповідає „нальоту частинки на стінку”. При цьому наближенні одержимо наступний розв’язок
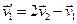 ,
,
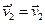 .
.
Переваги застосування 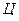 -системи проілюструємо на прикладі доведення співвідношень і , які раніше були отримані в
-системи проілюструємо на прикладі доведення співвідношень і , які раніше були отримані в 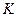 -системі.
-системі.
В 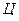 -системі і до, і після зіштовхування обидві частинки мають однакові за модулем і протилежні за напрямом імпульси
-системі і до, і після зіштовхування обидві частинки мають однакові за модулем і протилежні за напрямом імпульси
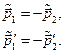
Більш того, внаслідок закону збереження сумарної кінетичної енергії частинок в результаті удару 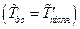 з урахуванням співвідношення одержимо
з урахуванням співвідношення одержимо
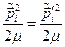 ,
,
тобто
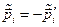 . Тут
. Тут 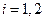 .
.
Останнє свідчить про те, що і швидкості кожної частинки в 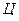 -системі рівні,
-системі рівні,
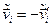 .
.
Тоді знайдемо 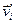 :
:
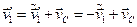 .
.
Підставимо сюди 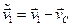 і отримаємо
і отримаємо
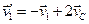 .
.
Дата добавления: 2015-06-17; просмотров: 1046;
