Пружній нелобовий удар куль. Векторна діаграма імпульсів

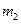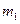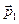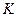Обмежимося випадком, коли друга частинка з масою до співудару знаходиться в стані спокою. Нехай частинка з масою і імпульсом в -системі утворила нелобовий пружній удар. Які можливі імпульси обох частинок після удару?

Розглянемо цей процес спочатку в 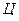-системі. Як і в розглянутому раніше лобовому співударі куль обидві частинки в любий момент часу до зіткнення мають однакові за модулем і протилежні за напрямом імпульси (дивись формулу ).

Неважко впевнитись, що і після зіткнення виконується таке ж співвідношення між імпульсами:

.

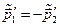Дійсно

,

.

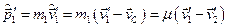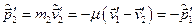Більше того, виявляється, що імпульс кожної частинки не змінюється за модулем в результаті зіткнення, тобто

.

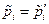Останнє твердження випливає із закону збереження кінетичної енергії при даному пружньому співударі куль. Правда це стосується 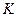-системи: 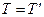. Використовуючи зв’язок між кінетичними енергіями в 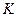- і 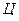-системах

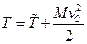
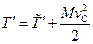
і враховуючи сталість величини 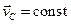, оскільки система двох частинок замкнена, із рівності 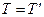отримуємо рівність кінетичних енергій до і після пружнього співудару і в 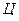-системі

.

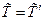Тут

,

.

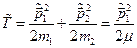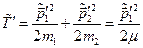Із рівності цих величин випливає рівність за модулем 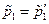(аналогічно доводиться 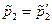), що і доводить формулу .

На відміну від лобового удару в даному випадку тільки напрям розльоту частинок зміниться. Він буде утворювати з напрямом руху частинок до співудару деякий кут 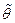, показаний на рис.52.

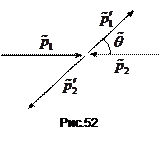Тепер знайдемо імпульси після зіткнення кожної частинки в 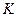-системі. За допомогою формул перетворення швидкостей при переході від 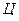- до 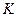-системи отримуємо

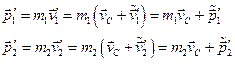
Тут 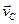– швидкість руху 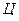-системи відносно 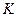-системи відліку. Складаючи окремо ліві і праві частини цих рівнянь, з врахуванням того, що 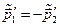, отримаємо

, ,

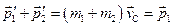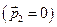як і повинно бути у відповідності із законом збереження імпульсу.

Побудуємо тепер векторну діаграму імпульсів. Спочатку намалюємо вектор 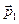відрізком 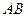(рис.53), потім вектори 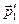і 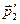, кожний із яких уявляє собою згдіно суму двох векторів. Ця побудова не залежить від кута 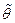. Звідси випливає, що точка 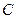може належати тільки колу радіуса 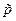з

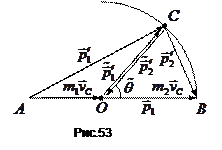
центром в точці 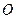, яка ділить відрізок 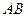на дві частини у відношенні 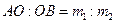. Більше того, у випадку, коли частинка 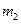покоїться до удару, коло повинно проходити через точку 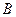– кінець вектора 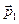, тому що відрізок 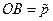. Доведемо це.

.

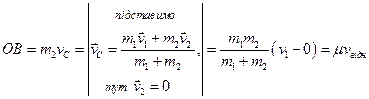З врахуванням формул і , а також , одержуємо

.

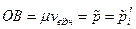Таким чином для побудови векторної діаграми імпульсів необхідно

1. відкласти відрізок 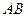, що відповідає імпульсу 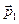частинки, яка налітає;

2. поділити відрізок 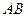точкою 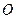у співвідношенні 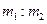і провести через точку 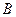з центром в точці 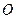коло радіусом .

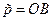Це коло є геометричне місце точок всіх можливих розташувань вершини 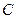трикутника імпульсів 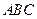, сторони якого 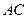і 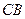уявляють собою можливі імпульси частинок після співудару (в 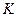-системі).

В залежності від співвідношення мас частинок точка 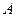– початок вектора 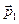–може знаходитись всередині кола, на колі і в його зовнішній області (рис.54). При цьому у всіх випадках кут 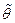може приймати всі значення від 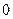до .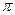

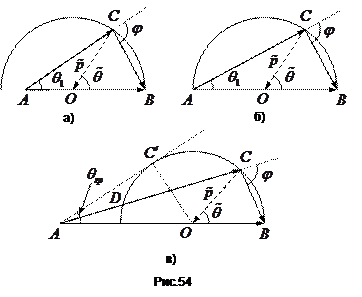
Можливі значення кута розсіяння 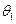частинки, що налітає, і кута розльоту 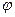частинки будуть такі

а)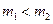
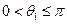
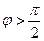
б)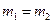
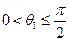
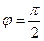
в)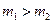

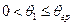
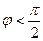
Тут 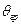– граничний кут. Він визначається формулою 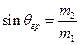, яка безпосередньо випливає з рис.54, в.

Звернемо увагу ще на один цікавий факт. В останньому випадку 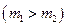для одного і того ж самого кута 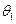можливе розсіяння частинки 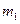як з імпульсом 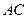, так і з імпульсом 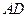(рис.54, в), тобто розв’язок в цьому випадку неоднозначний. Який саме розльот частинок реалізується? Для відповіді на це питання застосування тільки законів збереження недостатньо, треба звернутися до більш детального розгляду процесу зіткнення частинок із застосуванням рівнянь руху. Неоднозначність же розв’язку в даному випадку 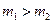пояснюється тим, що один і той же самий кут розсіяння 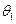може реалізуватися для двох значень прицільної відстані.