Обертання тіла навколо нерухомої осі
Нехай тіло з віссю, закріпленою в підшипниках, обертається з кутовою швидкістю  . Знайдемо спочатку вираз для моменту імпульсу твердого тіла відносно осі обертання (рис.57). Скориставшись формулою (5.3)
. Знайдемо спочатку вираз для моменту імпульсу твердого тіла відносно осі обертання (рис.57). Скориставшись формулою (5.3)
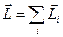
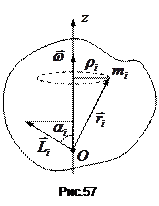 запишемо момент імпульсу
запишемо момент імпульсу  -ої частинки відносно довільної точки
-ої частинки відносно довільної точки 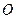 на осі
на осі
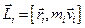 .
.
Тут 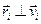 . Тому модуль вектора дорівнює
. Тому модуль вектора дорівнює
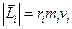 ,
,
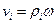 ,
, 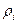 – найкоротша відстань від частинки
– найкоротша відстань від частинки 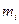 до осі обертання. Вектор
до осі обертання. Вектор 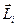 лежить в площині, що проходить через вісь обертання і частинку
лежить в площині, що проходить через вісь обертання і частинку 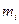 , і направлений під прямим кутом до вектора
, і направлений під прямим кутом до вектора 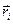 . Далі будемо знаходити проекції цих векторів на вісь обертання
. Далі будемо знаходити проекції цих векторів на вісь обертання
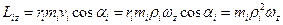 .
.
Просумувавши вираз по всім частинкам із яких складається тіло, одержимо проекцію моменту імпульсу тіла на вісь обертання. Це ще називають моментом імпульсу тіла відносно осі обертання
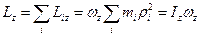 .
.
Величина 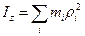 , яка за визначенням дорівнює сумі добутків елементарних мас на квадрати їх відстаней до осі обертання, називається моментом інерції тіла відносно даної осі. Із вигляду співвідношення випливає, що величина
, яка за визначенням дорівнює сумі добутків елементарних мас на квадрати їх відстаней до осі обертання, називається моментом інерції тіла відносно даної осі. Із вигляду співвідношення випливає, що величина 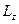 не залежить від того, де саме вибрати точку
не залежить від того, де саме вибрати точку 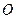 на осі обертання.
на осі обертання.
Оскільки абсолютно тверде тіло можна розглядати як систему матеріальних точок (частинок), то ми скористаємось рівнянням моментів (5.7), справедливим для любої системи частинок. В проекції на вісь 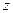 це рівняння має вигляд
це рівняння має вигляд
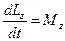 .
.
Підставивши сюди вираз для 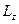 , прийдемо до рівняння, яке називається основним рівнянням динаміки обертання твердого тіла
, прийдемо до рівняння, яке називається основним рівнянням динаміки обертання твердого тіла
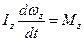 .
.
Тут 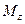 – сумарний момент всіх зовнішніх сил відносно осі обертання.
– сумарний момент всіх зовнішніх сил відносно осі обертання.
Рівняння аналогічне рівнянню 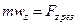 . Роль маси відіграє момент інерції, роль лінійного прискорення – кутове прискорення, а роль результуючої сили – сумарний момент зовнішніх сил. Таким чином, введений момент інерції характеризує інерційні властивості тіла відносно його обертання. Проявляються ці властивості, наприклад, в тому, що два стержня, підвішені за кінці (рис.58), під дією однакових моментів сил набувають таких кутових прискорень, які будуть обернено пропорційними моментам інерції цих стержнів:
. Роль маси відіграє момент інерції, роль лінійного прискорення – кутове прискорення, а роль результуючої сили – сумарний момент зовнішніх сил. Таким чином, введений момент інерції характеризує інерційні властивості тіла відносно його обертання. Проявляються ці властивості, наприклад, в тому, що два стержня, підвішені за кінці (рис.58), під дією однакових моментів сил набувають таких кутових прискорень, які будуть обернено пропорційними моментам інерції цих стержнів:
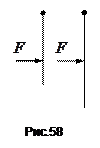
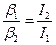 .
.
Зауважимо, що в загальному випадку вектор 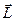 не співпадає за напрямком з віссю обертання тіла. І тільки для тіла, симетричного відносно осі обертання (для однорідного тіла обертання), момент імпульсу співпадає за напрямком з вектором
не співпадає за напрямком з віссю обертання тіла. І тільки для тіла, симетричного відносно осі обертання (для однорідного тіла обертання), момент імпульсу співпадає за напрямком з вектором 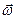 . В цьому випадку і, як побачимо далі, для несиметричного тіла при обертанні його навколо однієї із своїх головних осей інерції буде справедливе векторне співвідношення
. В цьому випадку і, як побачимо далі, для несиметричного тіла при обертанні його навколо однієї із своїх головних осей інерції буде справедливе векторне співвідношення
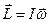 .
.
Дата добавления: 2015-06-17; просмотров: 1272;
