Момент інерції тіла відносно осі обертання
Із означення
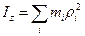
видно, що момент інерції є величина адитивна. Це означає, що момент інерції тіла дорівнює сумі моментів інерції його частин. Незважаючи не те, що поняття моменту інерції було введено при розгляді обертання твердого тіла, треба мати на увазі, що ця величина існує незалежно від того, обертається тіло чи ні. Практично розрахунок величини проводиться шляхом інтегрування.
Як приклад, розглянемо обчислення моменту інерції однорідного циліндра відносно осі, яка перпендикулярна до площини основи циліндра і проходить через його центр (рис.59).
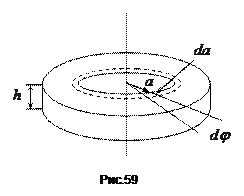 Визначимо елементарну масу
Визначимо елементарну масу 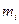 через густину речовини циліндра
через густину речовини циліндра 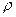 та елементарний об’єм
та елементарний об’єм 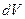 :
: 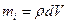 . Скористаємось виразом елементарного об’єму в полярній системі координат
. Скористаємось виразом елементарного об’єму в полярній системі координат 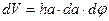 . Зміст величин
. Зміст величин 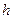 ,
, 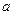 ,
, 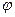 зрозумілий із позначень, наведених на рисунку. Задача сумування нескінченно малих величин в формулі зводиться до інтегрування:
зрозумілий із позначень, наведених на рисунку. Задача сумування нескінченно малих величин в формулі зводиться до інтегрування:
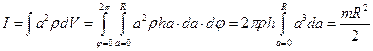
Тут введена маса циліндра 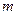 , що дорівнює добутку густини
, що дорівнює добутку густини 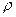 на об’єм циліндра
на об’єм циліндра 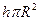 .
.
Моменти інерції деяких однорідних твердих тіл відносно осі 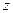 , що проходить через центр мас тіла, наведені в таблиці
, що проходить через центр мас тіла, наведені в таблиці
| Тверде тіло | Вісь 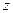
| Момент інерції |
Тонкий стержень довжини 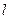
| Перпендикулярна стержню | 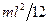
|
Суцільний циліндр радіуса 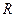
| Співпадає з віссю циліндра | 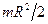
|
Тонкий диск радіуса 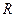
| Співпадає з діаметром диска | 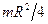
|
Куля радіуса 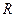
| Проходить через центр кулі | 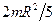
|
Кільце з внутрішнім 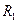 і зовнішнім і зовнішнім 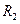 радіусами радіусами
| Співпадає з віссю кільця | 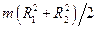
|
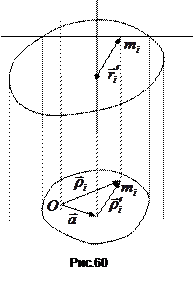 Розрахунки моментів інерції твердих тіл довільної форми відносно тієї чи іншої осі, взагалі кажучи, виявляються складними задачами. Навіть для згаданого раніше циліндра обчислення моменту інерції відносно осі, паралельної осі симетрії, але закріпленої на бічній поверхні, вже зазнає великих труднощів. В таких випадках знаходження моментів інерції полегшується, якщо скористатися теоремою Штейнера. Формулюється вона так. Момент інерції твердого тіла
Розрахунки моментів інерції твердих тіл довільної форми відносно тієї чи іншої осі, взагалі кажучи, виявляються складними задачами. Навіть для згаданого раніше циліндра обчислення моменту інерції відносно осі, паралельної осі симетрії, але закріпленої на бічній поверхні, вже зазнає великих труднощів. В таких випадках знаходження моментів інерції полегшується, якщо скористатися теоремою Штейнера. Формулюється вона так. Момент інерції твердого тіла 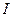 відносно довільної осі
відносно довільної осі 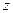 дорівнює моменту інерції
дорівнює моменту інерції 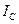 цього тіла відносно осі
цього тіла відносно осі 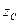 , паралельної даній і що проходить через центр мас тіла, плюс добуток маси тіла
, паралельної даній і що проходить через центр мас тіла, плюс добуток маси тіла 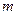 на квадрат відстані
на квадрат відстані 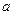 між осями
між осями
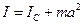 .
.
Для доведення теореми Штейнера проведемо через 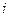 -ий елемент твердого тіла площину, перпендикулярну до осі
-ий елемент твердого тіла площину, перпендикулярну до осі 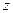 , і в цій площині – три вектори
, і в цій площині – три вектори 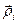 ,
, 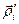 та
та 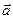 (рис.60). Перші два вектори характеризують положення елементарної маси
(рис.60). Перші два вектори характеризують положення елементарної маси 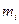 відносно осей
відносно осей 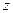 і
і 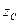 , а вектор
, а вектор 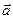 – положення осі
– положення осі 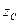 відносно осі
відносно осі 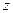 . Скориставшись зв’язком між цими векторами
. Скориставшись зв’язком між цими векторами 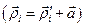 , перетворимо вираз для моменту інерції тіла відносно осі
, перетворимо вираз для моменту інерції тіла відносно осі 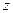 :
:
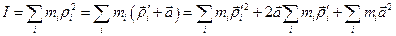 .
.
З правого боку цього рівняння перший член уявляє собою момент інерції тіла 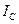 відносно осі
відносно осі 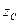 , а остання сума просто дорівнює
, а остання сума просто дорівнює 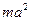 . Залишається довести, що середня сума дорівнює нулю.
. Залишається довести, що середня сума дорівнює нулю.
Нехай 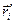 –радіус-вектор
–радіус-вектор 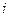 -го елемента тіла відносно центра мас, тоді відносно центра мас справедливе співвідношення
-го елемента тіла відносно центра мас, тоді відносно центра мас справедливе співвідношення 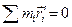 . Але
. Але 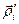 – вектор-проекція вектора
– вектор-проекція вектора 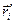 на площину, перпендикулярну до осі
на площину, перпендикулярну до осі 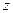 . Звідси ясно, якщо сумарний вектор дорівнює нулю, то і сума його векторів-проекцій на любу площину теж буде рівна нулю, тобто
. Звідси ясно, якщо сумарний вектор дорівнює нулю, то і сума його векторів-проекцій на любу площину теж буде рівна нулю, тобто 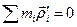 . Отже, теорему доведено.
. Отже, теорему доведено.
Дата добавления: 2015-06-17; просмотров: 3076;
