Обертання тіла навколо вільних осей

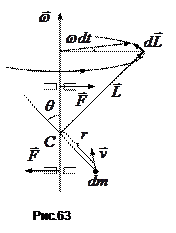Якщо тверде тіло привести у обертання навколо довільної осі (дивись рис.63) і не підтримувати його, то, взагалі кажучи, напрям осі обертання буде змінюватись. Щоб не змінювався напрям осі, треба утримувати її якимись силами, наприклад тими, що діють з боку підшипників.

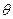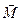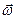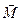Розглянемо це питання на прикладі обертання однорідного стержня. Скріпимо жорстко середину стержня з віссю обертання так, щоб кут між стержнем і віссю дорівнював (рис.63). Знайдемо момент зовнішніх сил, які необхідно прикласти до осі обертання, щоб при обертанні стержня з кутовою швидкістю її напрям не змінювався. Згідно з рівнянням (5.7) цей момент . Тобто, щоб знайти , треба спочатку знайти момент імпульсу стержня 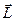, а потім його похідну по часу. Момент імпульсу простіше знайти відносно точки 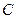. Виділимо елементарну масу 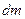, що знаходиться на відстані 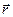від точки 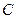. Момент імпульсу цієї маси відносно точки 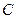дорівнює , де – швидкість елементарної маси. Легко бачити, що вектор 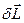направлений перпендикулярно до стержня і лежить в площині, утвореної стержнем і віссю обертання. Це справедливе для всіх елементарних мас. Тому сумарний момент імпульсу 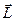стержня співпадає за напрямом з кожним з векторів .

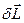Відмітимо, що в даному випадку вектор 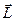не співпадає за напрямом з .

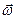При обертанні стержня вектор 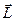теж обертається з кутовою швидкістю 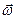. За інтервал часу 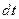вектор 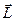отримає приріст , модуль якого, як видно із рис.63, дорівнює

,

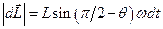або у векторному вигляді 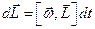. Поділивши на 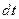, отримаємо

.

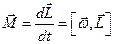Це і є той момент зовнішніх сил, який треба прикласти до осі, щоб під час обертання не змінювався її напрям. Сили, що утворюють цей момент, які діють на вісь з боку підшипників, показані на рис.63.

З аналізу рівняння бачимо, що при 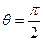вектор 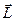співпадає за напрямом з 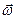, і в цьому випадку 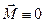, тобто напрям осі обертання буде залишатися незмінним без дії зовнішніх сил.

Саме така вісь обертання, напрям якої залишається незмінним без дії на неї зовнішніх сил, називається вільною віссю тіла. В загальній теорії доводиться, що для будь-якого твердого тіла, навіть несиметричного, існують три взаємно перпендикулярні осі, що проходять через центр мас тіла, які можуть служити вільними осями. Ці осі називаються головними осями інерції тіла. Знаходження їх – складна задача. Але задача спрощується, якщо тверде тіло має ту чи іншу симетрію. Головні осі інерції в цьому випадку просто співпадають з осями симетрії тіла.

Наприклад, у однорідного прямокутного паралелепіпеда головні осі інерції проходять через центри протилеглих граней. У тіла з осьовою симетрією (наприклад, у циліндра) фіксована лише одна із головних осей інерції, яка співпадає з віссю симетрії. Двома іншими осями інерції являються любі дві взаємно перпендикулярні осі, що лежать в площині, перпендикулярній до осі симетрії, і що проходять через центр мас. У тіла з центральною симетрією (наприклад, у кулі) головними осями інерції являються любі три взаємно перпендикулярні осі, що проходять через центр мас тіла.

Важливою особливістю головних осей інерції є те, що при обертанні навколо любої із них момент імпульсу 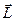тіла співпадає по напрямку з кутовою швидкістю 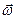тіла і визначається формулою 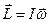. Тут 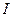– момент інерції тіла відносно даної головної осі інерції. Причому 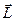не залежить від вибору точки на осі, відносно якої від визначається.

Підкреслимо ще раз, що в загальному випадку напрям вектора 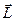не співпадає з вектором 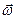і зв’язок між цими векторами носить складний характер. Ця обставина є причиною складної поведінки обертання твердих тіл.