Аналіз одномірного руху частинки в потенціальному полі сил
Застосування законів збереження
Одномірним називається рух частинки з одним ступенем вільності. Нехай частинка масою 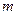 рухається в полі сил, яке описується потенціальною енергією
рухається в полі сил, яке описується потенціальною енергією 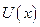 . Оскільки відмінною від нуля є лише одна компонента зовнішньої сили
. Оскільки відмінною від нуля є лише одна компонента зовнішньої сили 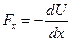 , то внаслідок закону збереження імпульсу, компоненти імпульсу частинки
, то внаслідок закону збереження імпульсу, компоненти імпульсу частинки 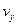 і
і 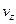 будуть залишатись сталими. В цьому випадку рівняння руху матиме вигляд
будуть залишатись сталими. В цьому випадку рівняння руху матиме вигляд
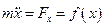
Але розв’язок такого рівняння безпосереднім інтегруванням є досить складною математичною задачею. Проте застосування законів збереження дає можливість провести якісне дослідження руху. Покажемо, що за допомогою закону збереження енергії можна якісно проаналізувати характер одномірного руху в довільному полі 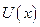 не розв’язуючи диференціальне рівняння .
не розв’язуючи диференціальне рівняння .
Закон збереження енергії для випадку одномірного руху має вигляд
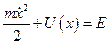 .
.
1)Оскільки кінетична енергія 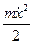 невід’ємна, то з випливає нерівність
невід’ємна, то з випливає нерівність
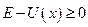 ,
,
яка накладає обмеження на можливі значення повної енергії 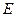 та координат частинки
та координат частинки 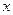 . Дійсно, для існування розв’язку нерівності відносно
. Дійсно, для існування розв’язку нерівності відносно 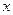 необхідно, щоб величини
необхідно, щоб величини 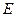 були більші за найменше можливе значення потенціальної енергії
були більші за найменше можливе значення потенціальної енергії 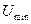 , тобто
, тобто
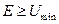 .
.
Області зміни значень 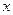 , при яких задовольняється нерівність називаються класично доступними.
, при яких задовольняється нерівність називаються класично доступними.
Точки 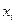 , у яких потенціальна енергія дорівнює повній енергії
, у яких потенціальна енергія дорівнює повній енергії
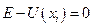 ,
, 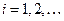
називаються точками зупинки. З випливає, що швидкість частинки 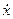 має задовольняти рівняння
має задовольняти рівняння
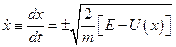 .
.
Згідно з при 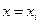 ,
, 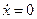 . Оскільки умова визначає границі класично доступних і класично недоступних областей, то в точках
. Оскільки умова визначає границі класично доступних і класично недоступних областей, то в точках 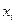 швидкість частинки змінює знак.
швидкість частинки змінює знак.
Якщо рух обмежений двома точками, то рух називається фінітним, якщо область руху необмежена чи обмежена одною точкою (тобто уявляє собою нескінчений інтервал), то рух частинки в такій області називають інфінітним. Проілюструємо сказане на прикладі потенціалу, зображеного на рис.50.
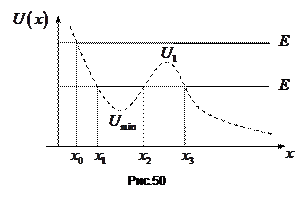 При
При 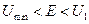 маємо дві класично доступні області
маємо дві класично доступні області 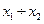 і
і 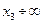 . В області
. В області 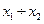 частинка здійснюватиме фінітний рух, а в області
частинка здійснюватиме фінітний рух, а в області 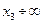 – інфінітний.
– інфінітний.
При 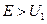 частинка буде утворювати тільки інфінітний рух в області
частинка буде утворювати тільки інфінітний рух в області 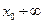 .
.
2)Користуючись законом збереження енергії у формі можна знайти залежність швидкості частинки від координати 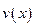 , якщо відома функція
, якщо відома функція 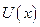 . Цю ж залежність можна використати для визначення залежності координати частинки від часу. Для цього в проведемо відокремлення змінних
. Цю ж залежність можна використати для визначення залежності координати частинки від часу. Для цього в проведемо відокремлення змінних
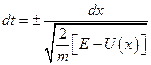 .
.
Звідси
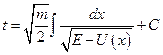 .
.
Розв’язуючи рівняння відносно 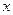 , дістанемо шукану залежність
, дістанемо шукану залежність 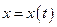 . Сталі
. Сталі 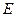 і
і 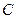 визначають за початковими значеннями координати і швидкості частинки.
визначають за початковими значеннями координати і швидкості частинки.
3)Одномірний фінітний рух частинки є періодичним – частинка періодично рухається між точками 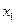 і
і 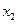 . Час руху
. Час руху 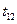 від
від 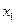 до
до 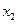 дорівнює часу руху
дорівнює часу руху 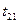 в зворотньому напрямку
в зворотньому напрямку
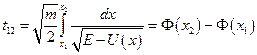 ;
;
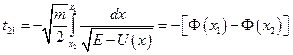 .
.
Тут 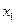 і
і 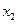 є розв’язками рівняння
є розв’язками рівняння 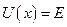 . Видно, що
. Видно, що 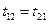 . Період коливань визначається як час, протягом якого частинка здійснює перехід між точками повороту
. Період коливань визначається як час, протягом якого частинка здійснює перехід між точками повороту 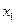 і
і 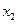
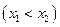 і назад
і назад
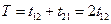 .
.
Отже, доведена періодичність фінітного руху.
4)Розглянемо малі коливання частинки поблизу мінімуму потенціальної енергії.
Розкладемо потенціальну енергію 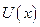 поблизу мінімуму у ряд Маклорена
поблизу мінімуму у ряд Маклорена
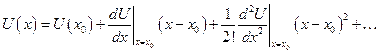
Приймемо 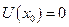 ,
, 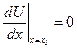 і позначимо
і позначимо 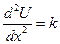 . Одержуємо
. Одержуємо
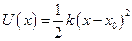 .
.
Позначимо 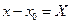 , тоді
, тоді 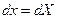 ,
, 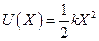 . Графіки цих функцій показані на рис. 51.
. Графіки цих функцій показані на рис. 51.
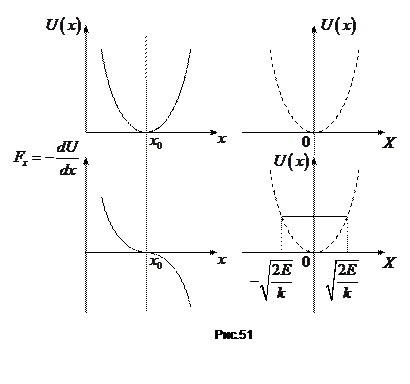
Для нової змінної 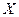 положення рівноваги частинки визначається її значенням
положення рівноваги частинки визначається її значенням 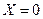 . Точки повороту визначаються умовою
. Точки повороту визначаються умовою 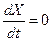 , тобто
, тобто 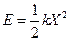 , звідки знаходимо
, звідки знаходимо
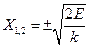 .
.
Знайдемо період коливань
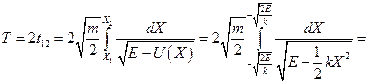
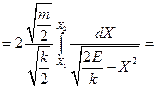
Згадуючи табличний інтеграл 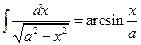 , маємо
, маємо
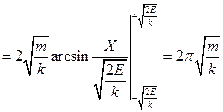 .
.
Дата добавления: 2015-06-17; просмотров: 1993;
