ВИЗНАЧЕННЯ ДОВЖИНИ ХВИЛІ ЗА ДОПОМОГОЮ ДИФРАКЦІЙНОЇ РЕШІТКИ
Явище дифракції світла полягає у відхиленні світлових хвиль від прямолінійного руху.
Це явище спостерігається у тих випадках, коли розміри перешкоди на шляху світла порівняні з довжиною хвилі. Тоді світло опиняється в області геометричної тіні, і спостерігається дифракційна картина чергування максимумів і мінімумів освітленості.
Явище дифракції зручно якісно розглядати, виходячи з принципу Гюйгенса. Відповідно до принципу Гюйгенса, кожна точка хвильового фронту розглядається як джерело другорядних хвиль; огинальна всіх другорядних хвиль для деякого моменту часу є хвильова поверхня для цього моменту.
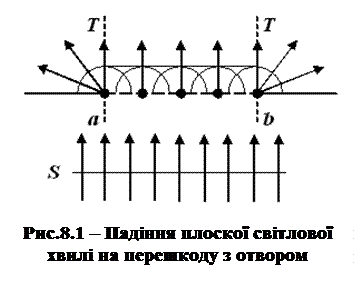 На рисунку 8.1 зображено отвір у непрозорому екрані, на який падає плоска світлова хвиля S. Ширина освітленої, з точки зору геометричної оптики, області ТТ дорівнює
На рисунку 8.1 зображено отвір у непрозорому екрані, на який падає плоска світлова хвиля S. Ширина освітленої, з точки зору геометричної оптики, області ТТ дорівнює 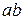 . Проте, відповідно до принципу Гюйгенса, кожна точка фронту
. Проте, відповідно до принципу Гюйгенса, кожна точка фронту 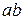 сама є джерело світлових хвиль. На рисунку 8.1 показано, що хвилі, випроменені поблизу точок а та b, заходять в область геометричної тіні. У цих місцях буде спостерігатися дифракційна картина.
сама є джерело світлових хвиль. На рисунку 8.1 показано, що хвилі, випроменені поблизу точок а та b, заходять в область геометричної тіні. У цих місцях буде спостерігатися дифракційна картина.
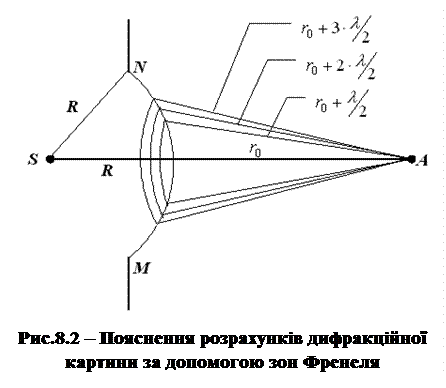
Для кількісних розрахунків дифракційної картини використовують спосіб зон Френеля. Істотність способу пояснюється за допомогою рисунку 8.2. Для розрахунку дії хвильового фронту MN у точці А розіб’ємо поверхню хвилі на кільцеві зони, проведемо на ній кола, центри яких знаходяться на одній осі. Кола проведемо таким чином, щоб відстань від точки А до сусідніх кіл відрізнялась на половину довжини хвилі 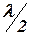 . Тоді коливання від кожних двох сусідніх зон Френеля надійдуть у точку А у протилежній фазі і при накладанні вони будуть взаємно послаблюватися.
. Тоді коливання від кожних двох сусідніх зон Френеля надійдуть у точку А у протилежній фазі і при накладанні вони будуть взаємно послаблюватися.
Площі усіх зон Френеля приблизно однакові:
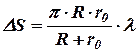 . (8.1)
. (8.1)
Амплітуди коливань, що приходять у точку А від різних зон, неоднакові:
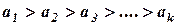 . (8.2)
. (8.2)
Тому приблизно можна вважати, що амплітуди коливань від кожної зони є півсума амплітуд від двох суміжних зон. Наприклад:
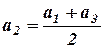 ,
, 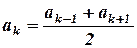 (8.3)
(8.3)
 У наслідок того, що коливання з амплітудами
У наслідок того, що коливання з амплітудами 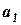 та
та 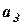 приходять у точку А в фазі, протилежній фазі коливань з амплітудою
приходять у точку А в фазі, протилежній фазі коливань з амплітудою 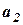 , то легко зрозуміти, що дія половини центральної зони сумісно з дією половини другої зони знищить дію першої зони і т. ін. Амплітуда, що створюється в довільній точці А всією сферичною хвильовою поверхнею дорівнює половині амплітуди, яка створюється однією центральною зоною:
, то легко зрозуміти, що дія половини центральної зони сумісно з дією половини другої зони знищить дію першої зони і т. ін. Амплітуда, що створюється в довільній точці А всією сферичною хвильовою поверхнею дорівнює половині амплітуди, яка створюється однією центральною зоною:
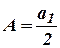 (8.4)
(8.4)
Якщо на шляху променя є непрозорий екран, що закриває частину зон, або отвір, який пропускає тільки визначену кількість зон, то необхідно провести конкретне сумування дій визначеної кількості зон.
Кількість зон, що знаходиться на частині хвильового фронту, яка не закрита екраном, залежить від відношення розмірів отвору до довжини хвилі і від його місцезнаходження:
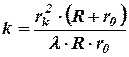 , (8.5)
, (8.5)
де 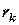 – радіус зовнішньої границі k-ої зони Френеля.
– радіус зовнішньої границі k-ої зони Френеля.
Дифракція від вузької щілини.
Дифракція на щілині являє собою окремий випадок дифракції Фраунгофера, що спостерігається в паралельних променях за допомогою лінз, які дають зображення дифракційної картини у фокальній площині.
 Нехай на щілину
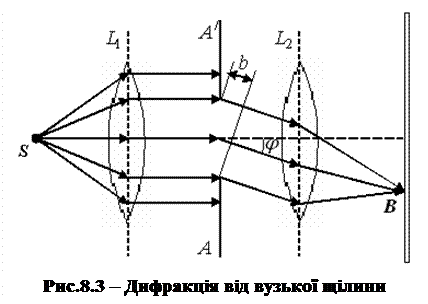
Нехай на щілину 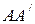 , що має сталу ширину а, падає паралельний пучок світла. Розглянемо промені, випущенні фронтом а у напрямку, що складає кут
, що має сталу ширину а, падає паралельний пучок світла. Розглянемо промені, випущенні фронтом а у напрямку, що складає кут 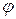 з початковим напрямом пучка (рис.8.3). Ці паралельні промені після проходження через лінзу зберуться у точці В на екрані в фокальній площині лінзи. Розіб’ємо фронт на зони Френеля так, як описано вище. У цьому випадку, очевидно, зони мають вигляд прямокутних смуг, паралельних до краю щілини.
з початковим напрямом пучка (рис.8.3). Ці паралельні промені після проходження через лінзу зберуться у точці В на екрані в фокальній площині лінзи. Розіб’ємо фронт на зони Френеля так, як описано вище. У цьому випадку, очевидно, зони мають вигляд прямокутних смуг, паралельних до краю щілини.
Розміри зон Френеля залежать від кута, під яким спостерігаємо світло, що пройшло крізь таку щілину. Усього на ній поміститься 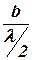 зон, де
зон, де 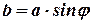 . Всі зони в заданому напрямку випромінюють світло цілком однаково. При інтерференції світла від кожної пари сусідніх зон амплітуда результуючих коливань дорівнює нулю, бо ці зони спричиняють коливання з однаковими амплітудами, але протилежними фазами. Отже, результат інтерференції світла в точці В визначиться тим, скільки зон Френеля вкладається в щілині.
. Всі зони в заданому напрямку випромінюють світло цілком однаково. При інтерференції світла від кожної пари сусідніх зон амплітуда результуючих коливань дорівнює нулю, бо ці зони спричиняють коливання з однаковими амплітудами, але протилежними фазами. Отже, результат інтерференції світла в точці В визначиться тим, скільки зон Френеля вкладається в щілині.
Якщо кількість зон парна ( 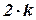 ), то
), то
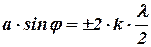 , де
, де 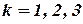 (8.7)
(8.7)
і в точці В спостерігаємо дифракційний мінімум. Знак „-” у правій частині відповідає променям світла, які поширюються від щілини під кутом 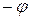 і збираються в побічному фокусі лінзи, який симетричний відносно головного фокусу.
і збираються в побічному фокусі лінзи, який симетричний відносно головного фокусу.
Якщо кількість зон непарна, то
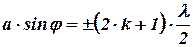 , (8.8)
, (8.8)
і в точці В отримуємо дифракційний максимум, який відповідає дії однієї зони Френеля. k – порядок дифракційного максимуму.
Дифракційна решітка
 Розглянемо дифракцію світла, обумовлену дією дифракційної решітки. Цей випадок дифракції найважливіший, бо його широко використовують у багатьох експериментальних методах спектрального аналізу світла. Дифракційна решітка – це система з великої кількості однакових за шириною і паралельних одна до одної щілин, що лежать в одній площині і відокремлені непрозорими проміжками, однаковими за шириною.
Розглянемо дифракцію світла, обумовлену дією дифракційної решітки. Цей випадок дифракції найважливіший, бо його широко використовують у багатьох експериментальних методах спектрального аналізу світла. Дифракційна решітка – це система з великої кількості однакових за шириною і паралельних одна до одної щілин, що лежать в одній площині і відокремлені непрозорими проміжками, однаковими за шириною.
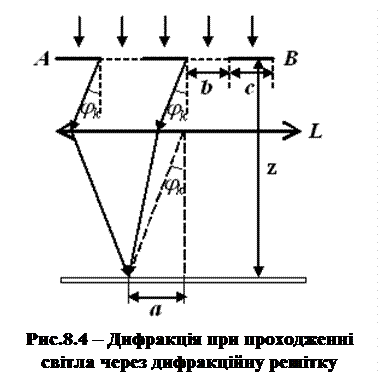
Розглянемо дифракцію плоскої монохроматичної хвилі, яка падає нормально на поверхню решітки АВ (рис.8.4). До всіх щілин хвиля надійде одночасно, тому можна вважати, що всі щілини решітки випромінюють другорядні хвилі в одній фазі. Результуюча амплітуда коливань, що падають на лінзу L під кутом 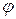 , дорівнює сумі амплітуд коливань від кожної щілини решітки, що падають на лінзу під цим кутом. Умови спостереження дифракційних максимумів мають вигляд:
, дорівнює сумі амплітуд коливань від кожної щілини решітки, що падають на лінзу під цим кутом. Умови спостереження дифракційних максимумів мають вигляд:
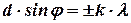 , (8.9)
, (8.9)
де 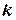 – ціле число;
– ціле число; 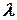 – довжина хвилі світла;
– довжина хвилі світла; 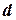 – постійна дифракційної решітки.
– постійна дифракційної решітки.
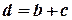 , (8.10)
, (8.10)
де 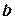 – ширина щілини, с – ширина непроникної для світла ділянки між двома щілинами. Оскільки місцезнаходження дифракційного максиму залежить від довжини хвилі, то у випадку, коли на дифракційну решітку падає не монохроматичне світло, воно розкладається на складові кольори. Світлові хвилі, що мають різну довжину хвилі, за дифракційною решіткою поширюються у різних напрямках.
– ширина щілини, с – ширина непроникної для світла ділянки між двома щілинами. Оскільки місцезнаходження дифракційного максиму залежить від довжини хвилі, то у випадку, коли на дифракційну решітку падає не монохроматичне світло, воно розкладається на складові кольори. Світлові хвилі, що мають різну довжину хвилі, за дифракційною решіткою поширюються у різних напрямках.
 Отже, дифракційна решітка є спектральним апаратом. За її допомогою можна розкладати світло на складові кольори і визначати склад світлових променів. Співвідношення (8.9) дає можливість по відомому періоду решітки і експериментально виміряному куту розрахувати довжину світлової хвилі
Отже, дифракційна решітка є спектральним апаратом. За її допомогою можна розкладати світло на складові кольори і визначати склад світлових променів. Співвідношення (8.9) дає можливість по відомому періоду решітки і експериментально виміряному куту розрахувати довжину світлової хвилі 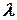 . Вимірювання довжини хвилі зводиться до експериментального визначення кута
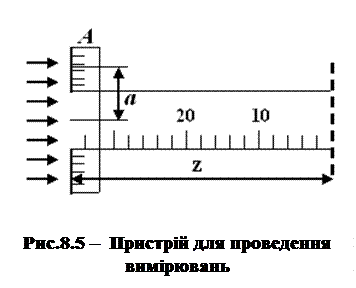
. Вимірювання довжини хвилі зводиться до експериментального визначення кута 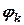 , під яким спостерігається дифракційний максимум. Схематичний пристрій, за допомогою якого спостерігається спектральний склад випромінювання, зображено на рисунку 8.5.
, під яким спостерігається дифракційний максимум. Схематичний пристрій, за допомогою якого спостерігається спектральний склад випромінювання, зображено на рисунку 8.5.
Природне світло проходить крізь щілину у металевій лінійці А, на яку нанесено шкалу. Потім промінь проходить крізь дифракційну решітку і дифрагує. Спостереження ведеться оком. Роль лінзи грає оптична система ока. Око бачить спектри, що локалізовані поблизу шкали. На шкалі можна виміряти ширину спектра, тобто від смуги, що відповідає визначеній 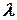 , до нульового порядку, тобто до щілини у пластинці. Знаючи цю величину і відстань від шкали до решітки можна визначити довжину хвилі. Нехай ширина спектра при довжині хвилі
, до нульового порядку, тобто до щілини у пластинці. Знаючи цю величину і відстань від шкали до решітки можна визначити довжину хвилі. Нехай ширина спектра при довжині хвилі 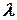 дорівнює a, а відстань від щілини до решітки – z. При малих кутах:
дорівнює a, а відстань від щілини до решітки – z. При малих кутах:
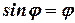 . (8.11)
. (8.11)
Із формули (8.9) отримаємо
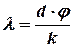 . (8.12)
. (8.12)
З іншого боку, з рисунку 8.4 видно, що
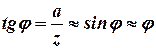
або 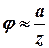 (8.13)
(8.13)
Підставляючи в (8.12), отримаємо
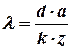 . (8.14)
. (8.14)
Дата добавления: 2015-04-10; просмотров: 7585;
