Векторні хвилі. Поляризація
Нехай деяка векторна величина 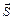 (наприклад, швидкість
(наприклад, швидкість 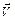 , напруженість
, напруженість 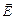 електричного поля або напруженість
електричного поля або напруженість 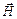 магнітного поля і т.п.) є функцією координат і часу. Обмежимося випадком плоского недеформірованной хвилі
магнітного поля і т.п.) є функцією координат і часу. Обмежимося випадком плоского недеформірованной хвилі 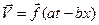 .
.
Якщо вектор 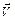 перпендикулярний до напрямку поширення хвилі (тобто до осі
перпендикулярний до напрямку поширення хвилі (тобто до осі 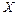 ), хвиля називається поперечною, якщо вектор
), хвиля називається поперечною, якщо вектор 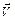 паралельний напряму поширення, хвиля називається поздовжньою. У загальному випадку вектор
паралельний напряму поширення, хвиля називається поздовжньою. У загальному випадку вектор 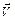 має і подовжню і поперечну складові.
має і подовжню і поперечну складові.
Випадок поздовжньої векторної хвилі мало відрізняється від випадку скалярної хвилі. Замість вектора 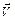 тут можна розглянути скаляр
тут можна розглянути скаляр 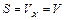 .
.
Окремим випадком поперечної хвилі є той, коли вектор 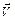 має в усіх точках простору однаковий і постійний в часі напрямок. Маючи, наприклад, вісь
має в усіх точках простору однаковий і постійний в часі напрямок. Маючи, наприклад, вісь 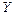 вздовж цього напрямку, зміну вектора
вздовж цього напрямку, зміну вектора 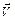 можна описати завданням скаляра
можна описати завданням скаляра 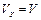 . Але цей випадок принципово відрізняється від скалярної хвилі, так як різні напрями, перпендикулярні до напрямку її поширення не є рівноправними між собою (наприклад, напрямки вздовж осей
. Але цей випадок принципово відрізняється від скалярної хвилі, так як різні напрями, перпендикулярні до напрямку її поширення не є рівноправними між собою (наприклад, напрямки вздовж осей 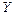 і
і 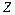 ).
).
Розглянемо більш загальний випадок поперечної хвилі. Назвемо синусоїдальною поперечною хвилею таку, яка описується рівняннями:
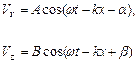 , (8.29)
, (8.29)
де 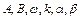 постійні.
постійні.
Відповідними перетвореннями виразів (8.29) можна довести, що кінець вектора 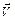 при фіксованому
при фіксованому 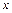 описує еліпс (рис.8.4), рівняння якого має вигляд:
описує еліпс (рис.8.4), рівняння якого має вигляд:
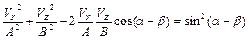 . (8.30)
. (8.30)
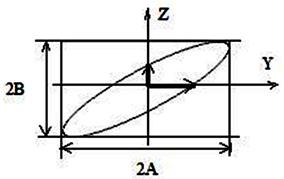
Рисунок 8.4 – Графік ілюстрації еліптичної поляризації
У цьому випадку говорять, що синусоїдальна поперечна хвиля еліптично поляризована. Зокрема, якщо 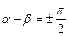 ,
, 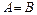 , то еліпс (8.30) ставати окружністю і тоді говорять, що хвиля поляризована по колу. У кожен момент часу
, то еліпс (8.30) ставати окружністю і тоді говорять, що хвиля поляризована по колу. У кожен момент часу 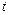 кінці вектора
кінці вектора 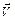 , пов'язані з різними точкам будь-якої прямої, паралельної осі
, пов'язані з різними точкам будь-якої прямої, паралельної осі 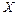 , розташовані по гвинтовій лінії. Зі зміною часу ця гвинтова лінія переміщується вздовж осі
, розташовані по гвинтовій лінії. Зі зміною часу ця гвинтова лінія переміщується вздовж осі 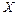 не обертаючись і не деформуючись (рис. 8.5, б). Тут же легко зрозуміти «ліву» і «праву» поляризації.
не обертаючись і не деформуючись (рис. 8.5, б). Тут же легко зрозуміти «ліву» і «праву» поляризації.
Якщо 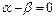 , або ,
, або , 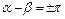 і
і 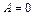 або
або 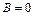 , то еліпс вироджується в пряму лінію. Таку хвилю називають лінійно-поляризованою (рис. 8.5, а).
, то еліпс вироджується в пряму лінію. Таку хвилю називають лінійно-поляризованою (рис. 8.5, а).
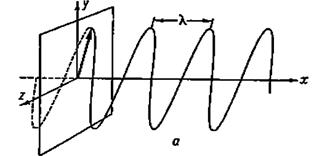

Рисунок 8.5 – Геометричне уявлення лінійно-поляризованої хвилі і хвилі, поляризованої по колу
КОНТРОЛЬНІ ЗАПИТАННЯ І ЗАВДАННЯ ДО РОЗДІЛУ 8
1. У чому полягає відмінність між хвильовим фронтом і хвильовою поверхнею?
2. Визначити як змінюється щільність матеріалу пружного стержня при поширенні в ньому плоскої хвилі.
3. Знайти залежність амплітуди сферичної хвилі від відстані 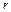 .
.
4. Знайти залежність амплітуди циліндричної хвилі від відстані 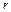 .
.
Дата добавления: 2015-06-12; просмотров: 1073;
