Загальні відомості плоского електромагнітного поля

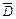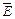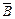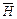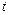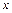Нехай , , , залежать від і . Розкладемо вектори 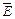і 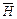на три перпендикулярних вектора, колінеарних осям координат. Для 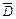і 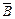маємо:

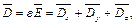(9.5)

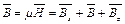, (9.6)

де кожна складова 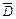і 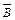дорівнює відповідно складово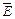ї і 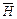, помноженої на скаляр 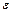або .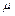

Обмежимося випадком ідеального діелектрика 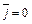і притому незарядженого ( 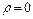).Рівняння (9.1) - (9.4) легко спрощуються.

У якості «допоміжної поверхні» візьмемо поверхню паралелепіпеда висоти 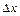з квадратною основою, сторони якого паралельні осям 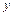і 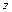і мають однакову довжину, рівну одиниці.

Застосування до нашої допоміжної поверхні рівнянь (9.1) - (9.4) приводить до наступної системи рівнянь:

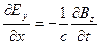, (9.7)

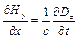, (9.8)

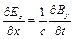, (9.9)

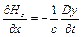, (9.10)

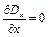, (9.11)

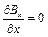, (9.12)

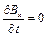, (9.13)

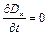, (9.14)

Рівняння (9.11), (9.14) і (9.12), (9.13) показують, що величини 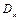і 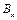залишаються постійними. Крім того рівняння (9.7), (9.14) не встановлюють ніякого зв'язку між собою, а також з усіма іншими компонентами полів 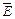і .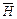

Це фізично означає наступне: плоске електромагнітне поле, яке залежить від 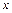, є суперпозицією однорідного електростатичного поля, паралельного осі 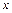і незалежного від нього однорідного статичного магнітного поля, також паралельного осі 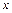і незалежного від цих двох полів електромагнітного поля, вектори 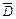, , 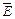, 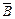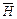якого мають тільки 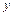і 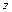компоненти (тобто перпендикулярні осі ).

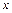Нас будуть цікавити тільки електромагнітні поля, що поширюються. Враховуючи вищесказане, приходимо до важливого результату: розповсюджуване плоске поле є поперечним полем, в ньому вектори 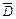, , 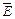, 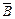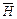лежать у площинах, перпендикулярних до напрямку поширення.