Плоскі хвилі

Зауважимо, що розповсюджуване плоске поле є суперпозицією двох не пов'язаних між собою полів:

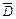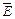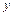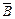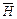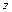а) поля, в якому вектори , колінеарні осі , а вектори , осі [рівняння (9.7), (9.10)].

Так як 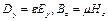, то (9.7), (9.10) можуть бути замінені наступними:

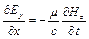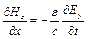, . (9.15)

б) поля, в якому 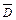, 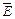колінеарні осі 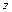, а вектори 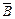, 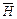осі 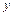. Аналогічно з (9.8), (9.9) одержимо

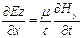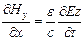, . (9.16)

Поле, що описується рівняннями (9.15), назвемо 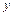-полем (по тому, як спрямований в ньому вектор 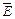), а поле (9.16) 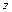-полем.

Кожне з цих полів не є ні чисто електричним, ні чисто магнітним, обидва є електромагнітними полями.

Розглянемо спочатку 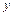-поле. З рівнянь (9.15) легко отримати

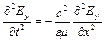. (9.17)

Це хвильове рівняння. Електрична компонента 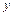- хвилі поширюється у вигляді хвилі, що деформується, зі швидкістю:

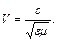
Тут же отримуємо для компоненти 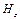рівняння

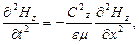(9.18)

тобто магнітна складова 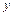- поля поширюється з тією ж швидкістю, що і електрична компонента.

Таким чином, замість « 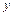- поля» можна говорити « - хвиля».

Використовуючи рішення хвильових рівнянь (9.17), (9.18) у вигляді гармонійних функцій можна знайти, що

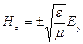. (9.19)

Тобто в кожній точці і в кожний момент часу магнітна компонента пропорційна електричній компоненті.

Для 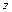- хвилі аналогічно виходить:

.

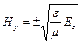як в 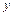- хвилі так і в 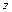- хвилі вектори 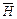, 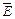перпендикулярні один до одного і до напрямку поширення (див. рис. 9.1).

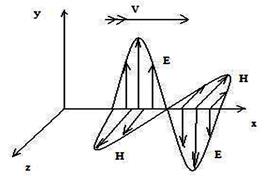
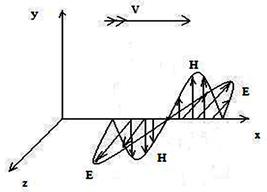
Рисунок 9.1 - Уявлення про структуру поля в електромагнітних y- і z-хвилях