ВИВЧЕННЯ ПРОСТОРОВОЇ РЕШІТКИ
До цього часу ми вивчали зовнішню форму кристалів та описували її особливою кристалографічною мовою. Однак, наявність граней та ребер кристалів і закони їх взаємного розташування є макроскопічним проявом закономірної внутрішньої структури кристалічних речовин. Строго математично це доведено законом Гаюі.
Просторова кристалічна решітка (рис. 5.1), у вузлах якої розташовані атоми, іони або молекули, складається з безкінечної множини рівних за величиною та формою паралелепіпедів, які можуть бути суміщені один з одним простим паралельним переносом (трансляцією).
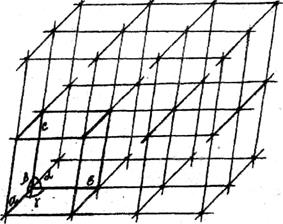
Рис. 5.1. Просторова решітка з елементарною коміркою
Паралелепіпед повторюваності, що називається елементарною коміркою, характеризується параметрами (ребрами) a, b, c та кутами між ними 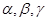 .
.
Параметри елементарної комірки змінюються в залежності від сингонії і точно співпадають з одиничними параметрами та кутами між координатними осями в правилах установки кристалів (табл. 3.1).
За характером розташування однакових атомів у комірці та за типом симетрії вся різноманітність структур підрозділяється на 14 просторових решіток Браве (табл.5.1). Сім з них примітивні (Р), по одній в кожній сингонії та сім складних: базоцентровані (С), гранецентровані (F) тa об'ємноцентровані (J).
У тому випадку, коли комірки, виділені за різними атомами не співпадають за типом, елементарна комірка, що характеризує структуру вважається примітивною.
Таблиця 5.1
14 типів решіток Браве 
| Сингонія | Типи решіток Браве | ||||
| Примітивна Р | Базоцентрована С | Об’ємноцентрована F | Гранецентрована J | Параметри елементарної комірки | |
| Триклинна | 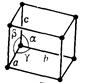
| а 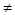 в в 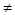 с с
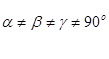
| |||
| Моноклинна | 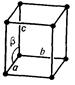
| 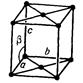
| а 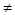 в в 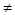 с с
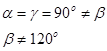
|
Продовження табл. 5.1
| Ромбічна | 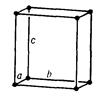
| 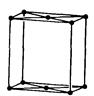
| 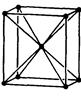
| 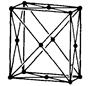
| а 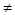 в в 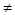 с с
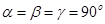
|
| Тригональна (ромбоедрична) | 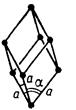
| а=в=с
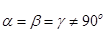
| |||
| Тетрагональна | 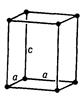
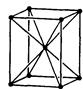
| 
| а=в 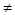 с с
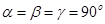
| ||
| Гексагональна | 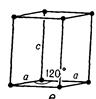
| а=в 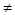 с с
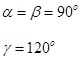
| |||
| Кубічна | 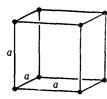
| 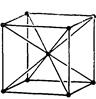
| 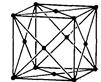
| а=в=с
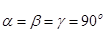
|
Більш детальна класифікація структур здійснюється за 230 групами симетрії Федорова
Для підрахунку кількості атомів, що припадає на одну елементарну комірку, необхідно враховувати наступне.
Кожен атом, що розташований у вершині комірки, належить одночасно вісьмом, коміркам; отже, на одну комірку припадає 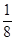 його частина. 8 атомів, розташованих по вершинах елементарної комірки, в сумі складають один, що належить даній комірці (
його частина. 8 атомів, розташованих по вершинах елементарної комірки, в сумі складають один, що належить даній комірці ( 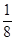 ∙ 8 = 1).Якщо атоми розташовуються на ребрах, то на комірку припадає
∙ 8 = 1).Якщо атоми розташовуються на ребрах, то на комірку припадає 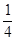 частина реберних атомів; якщо на гранях –
частина реберних атомів; якщо на гранях – 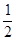 . Атоми, що знаходяться в середині комірки, належать їй цілком.
. Атоми, що знаходяться в середині комірки, належать їй цілком.
При вивчені структур складних речовин, наприклад, NaCl, окремо підраховується формульна одиниця для іонів натрію, окремо для іонів хлору та виводиться кількість структурних одиниць, тобто Z 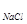 , що належать одній елементарній комірці:
, що належать одній елементарній комірці:
Z 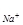 =
= 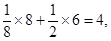
Z 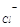 =
= 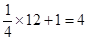
Z 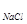 =4.
=4.
Важливими характеристиками при описі кристалічних структур є координаційне число та координаційний багатогранник.
Число атомів (іонів протилежного знаку), що складають найближче оточення даного атома (іона), називається координаційним числом, а геометрична фігура, одержана при сполученні центрів атомів (іонів), називається координаційним багатогранником.
Стійкість того чи іншого типу координації визначається співвідношенням іонних радіусів катіона (rk) та аніона (ra) (табл. 5.1).
Для стійкості кристалічної решітки потрібна умова мінімуму потенціальної енергії. Одним з факторів, що зменшують потенціальну енергію, є максимальне зближення структурних одиниць, їх найщільніша упаковка. Тенденція до найщільнішої упаковки притаманна всім типам кристалічних структур, але найбільш сильно вона виражена в іонних та металевих структурах.
Таблиця 5.2
Залежність координаційного числа від співвідношення іонних радіусів rk/ra
| Координаційні числа | Координаційні багатогранники | Границі відношення rk/ra |
| Гантель | 0-0,15 | |
| Трикутник | 0,15-0,22 | |
| Тетраедр | 0,22-0,41 | |
| Октаедр | 0,41-0,73 | |
| Куб | 0,73-1,0 | |
| Кубооктаедр | Більше 1,0 |
Якщо умовно уявити собі атоми або іони у вигляді сферичних куль, то в плоскому шарі кулі укладаються найщільніше так, що кожна куля оточена шістьома кулями та шістьома ямками, а кожна ямка – трьома кулями (рис. 6.1). Другий шар куль укладається, закриваючи половину ямок.
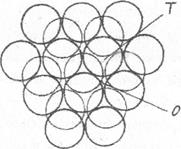
Рис.5.2. Упаковка рівновеликих куль у двох плоских шарах
Між двома шарами куль утворюються два типу порожнин, які відрізняються по координаційному оточенню. Порожнини першого типу – Т (ненаскрізні) утворюються трьома кулями одного шару і ще однією кулею, що знаходиться над (або під) порожниною. Така порожнина називається тетраедричною, оскільки центри чотирьох куль утворюють правильний тетраедр.
Порожнини другого типу – О (наскрізні) утворені трьома кулями одного шару та трьома кулями другого шару. Центри куль утворюють октаедр і порожнина називається октаедричною.
Третій шар цієї упаковки можна укласти двояким шляхом. Перший шлях – це укладання куль третього шару по ненаскрізних ямках. Таким чином, щоб вони були точно над кулями першого шару. Утворюється гексагональна упаковка типу АВ//АВ... . Така упаковка має одну вісь симетрії третього порядку.
Якщо укласти кулі третього шару в наскрізні ямки, то не 3-й шар повторить конфігурацію першого, а лише четвертий. Виходить упаковка типу ABC//ABC... Така упаковка має чотири осі симетрії L3. Упаковка називається кубічною і відповідає гранецентрованій кубічній решітці.
У випадку складних структур формування найщільніших упаковок проводиться аналогічним способом більш крупкими структурними одиницями – аніонами; катіони розміщуються в порожнинах. Наприклад, в структурі кам'яної солі аніони хлору утворюють кубічну найщільнішу упаковку, а катіони натрію займають всі октаедричні порожнини; тетраедричні залишаються незаповненими.
В обох типах найщільніших упаковок число тетраедричних порожнин вдвічі більше числа куль упаковки, а число октаедричних порожнин дорівнює числу куль упаковки. Атом чи іон, що займає тетраедричну порожнину, має координаційне число 4, а атоми, що займають октаедричну порожнину 6. Найщільніші упаковки слід шукати в структурах, що мають осі L 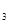 (в тригональній, гексагональній, кубічній).
(в тригональній, гексагональній, кубічній).
При описуванні структур у термінах найщільніших упаковок необхідно додержуватись наступного порядку роботи:
– відшукати в структурах L 3, (кубічній 4L 3);
– в площині перпендикулярній L 3, розглянути шари атомів. Якщо кожен атом оточений шістьома однойменними атомами, а атоми верхнього шару укладаються між кулями вихідного шару, тобто під кожним атомом (іоном) в вищележачих шарах знаходиться пустота, то шари повинні бути укладені найщільніше. Кубічну найщільнішу упаковку можна розпізнати, тому що це решітка типу F;
– визначити тип упаковки (в кубічній сингонії може бути лише кубічна найщільніша упаковка, а в тригональній та гексагональній – лише гексагональна);
– знайти тетраедричні та октаедричні порожнини в упаковці. Якщо структура іонна, визначити, які порожнини та яка їх частина зайнята катіонами.
При підрахунку частки заповнених порожнин слід дотримуватися такого порядку. Число куль упаковки позначимо N. Звичайно, найщільнішу упаковку утворюють крупні аніони. Тому приймаємо, що N = Z аніона (формульна одиниця аніона). Z катіонів, що мають координаційне число 4, позначимо К. Тоді частка заповнених тетраедричних порожнин складає K/2N. Z катіонів, що мають координаційне число 6, позначимо L. Тоді частка заповнених октаедричних порожнин складає L/N.
Завдання. При одержанні моделей кристалічних речовин Вам необхідно провести їх опис за такою схемою:
– виділення елементарної комірки, визначення сингонії та типу решітки Браве;
– підрахунок кількості структурних одиниць в одній елементарній комірці;
– визначення координаційних чисел та багатогранників; типу зв'язку;
– виділення найщільнішої упаковки. Якщо структура іонна, підрахунок частки заповнених порожнин.
Дата добавления: 2015-06-27; просмотров: 2070;
