Вимушені коливання

Розглянемо коливання, які здійснює матеріальна точка, якщо на неї, крім пружної сили і сил опору, діє додаткова періодична сила. Такі коливання називаються вимушеними. Прикладом може бути важок, який коливається на пружині і додатково підштовхується через рівні проміжки часу. Змінна зовнішня сила, яка прикладена до системи і зумовлює вимушені механічні коливання, називається змушувальною силою.

Розглянемо вимушені коливання найпростішої лінійної системи – пружинного маятника. Нехай рух відбувається вздовж осі ОХ під дією зовнішньої змінної сили 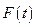, яка є періодичною функцією часу. Запишемо диференційне рівняння руху маятника

.

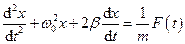Після застосування до маятника зовнішньої сили спочатку виникає перехідний режим вимушених коливань, тобто маятник поступово розгойдується під дією зовнішньої періодичної сили. Маятник при цьому бере участь в двох коливаннях:

.

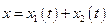Перший доданок відповідає власним загасальним коливанням, які завжди збуджуються у системі при дії зовнішньої сили. Ці коливання відбуваються на частоті 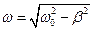. Другий доданок відповідає незагасальним періодичним коливанням маятника з частотою, яка дорівнює частоті змушувальної сили.

З плином часу після вмикання змушувальної сили перший доданок 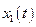загасає за експоненціальним законом. Отже, через деякий час доданок 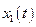практично зникне, і коливання системи будуть визначатись лише другим доданком 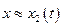. Характерний час загасання, як відомо, становить 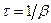. Цей час якраз і визначає тривалість перехідного режиму встановлення вимушених коливань у системі. Таким чином, чим менше загасання у системі, тим довше вона розгойдується, і навпаки, чим більше у системі тертя, тим швидше у ній встановлюються вимушені коливання.

Після закінчення перехідного режиму вимушені коливання встановляться, тобто подальше зростання їх амплітуди припиниться. Кажуть, що при цьому коливальна система перейде в стан встановлених вимушених коливань, які здійснюються з частотою змушувальної сили.

Якщо змушувальна сила змінюється за гармонічним законом, тобто 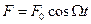, то встановлені вимушені коливання є також гармонічними з тією самою частотою:

.

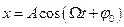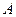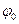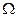Ця функція є розв’язком диференційного рівняння руху маятника (у цьому можна впевнитись підстановкою). Амплітуда встановлених вимушених коливань та зсув фаз між зміщенням та змушувальною силою залежать від співвідношення між циклічними частотами вимушених коливань та вільних незагасальних коливань :

, .

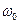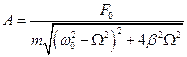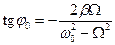Звідси видно, що в загальному випадку коливання відбувається не “в фазі” з силою. Тобто, максимального зміщення точка досягає не у той момент, коли сила найбільша. Якщо опір у системі дорівнює нулеві ( 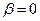), то встановлені вимушені коливання і сила мають однакові фази (щоправда, такі коливання мають нескінченно великий час розгойдування 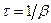). В усіх інших випадках зсув фаз між ними .

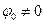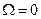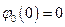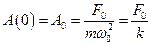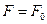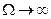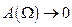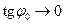Проаналізуємо залежності амплітуди і фази вимушених коливань від циклічної частоти змушувальної сили. При отримаємо і – статичне зміщення точки з положення рівноваги під дією сталої сили . При амплітуда і , а 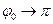. Графіки залежностей 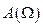і 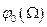наведено на рис.9.16. Амплітуда вимушених коливань має максимум при частоті змушувальної сили 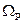, яка задовольняє співвідношення:

,

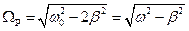де 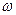– циклічна частота вільних загасальних коливань точки. Поява такого максимуму являє собою явище резонансу. Таким чином, зростання амплітуди вимушених коливань при наближенні циклічної частоти змушувальної сили до 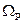є явищем механічного резонансу. Відповідно, частота 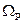називається резонансною частотою, а графіки залежності 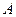від 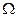, наведені на рис.9.16, – амплітудними резонансними кривими. Графіки залежності 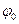від 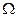називаються фазовими резонансними кривими.

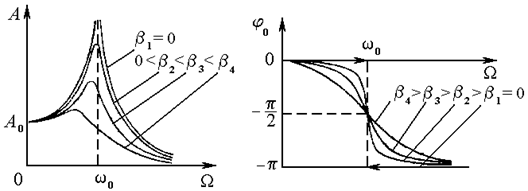
Рис.9.16.

Максимальна амплітуда вимушених коливань спостерігається при резонансі і дорівнює

,

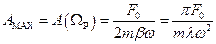де 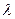– логарифмічний декремент загасання.

Якщо опір середовища дорівнює нулеві, тобто 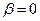, то максимум амплітуди виникає при 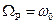. При цьому, якщо частота змушувальної сили стає рівною частоті 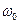власних коливань, амплітуда вимушених коливань стає нескінченно великою. При наявності опору середовища ( 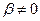) амплітуда ніколи не досягне нескінченності, і її максимум буде спостерігатись при частотах 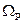змушувальної сили менших за 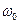. Чим більша величина 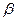, тим менш гостріший максимум, і менша резонансна частота.

Швидкість точки при встановлених вимушених гармонічних коливаннях

.

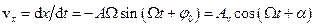Тут 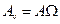і 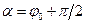– амплітуда швидкості і зсув фаз між швидкістю та змушувальною силою, причому

,

.

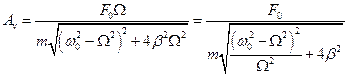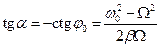Амплітуда швидкості максимальна при 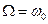і дорівнює

.

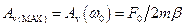В такому випадку 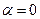, тобто швидкість точки коливається в одній фазі зі змушувальною силою. При 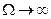амплітуда 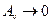і 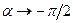, а при 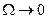амплітуда 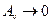і .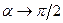

Прискорення точки при встановлених вимушених гармонічних коливаннях

.

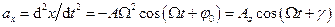Тут 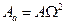і 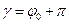– амплітуда прискорення і зсув фаз між прискоренням та змушувальною силою, причому

.

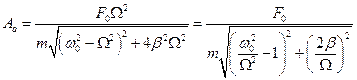Амплітуда прискорення максимальна при

.

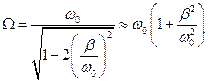При 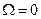амплітуда 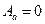, а при 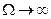амплітуда прискорення наближається до величини .

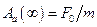При встановлених вимушених коливаннях втрати енергії коливною системою, які зумовлені дисипативними силами, повністю компенсуються за рахунок роботи, що виконується змушувальною силою. Наприклад, робота, що виконується за одне коливання силою опору, яка діє на пружинний маятник,

,

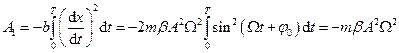де 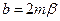– коефіцієнт опору.

Робота, що виконується за такий самий проміжок часу змушувальною силою ,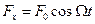

,

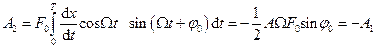оскільки .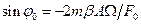

Робота зовнішньої сили максимальна при зсуві фаз 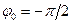, тобто при частоті, близькій до резонансної. При інших зсувах фаз сила частково діє прискорювально, а частково протидіє руху. При 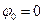або 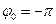сила протягом половини часу прискорює рух, а протягом іншої половини часу вона протидіє руху, тобто в середньому її робота дорівнює нулю. Звідси випливає, що поза областю резонансу змушувальна сила виконує лише незначну роботу, а при резонансі ця робота зростає. Такий ефект максимально помітний при гострому резонансі, коли .

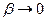Якщо змушувальна сила, що діє на пружинний маятник, змінюється періодично, але не за гармонічним законом, то її можна подати як суму гармонік цієї сили. Вони мають різні амплітуди, початкові фази і циклічні частоти, кратні 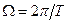, де 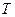– період зміни змушувальної сили. Оскільки маятник є лінійною коливною системою, то кожна з гармонік змушувальної сили діє таким чином, ніби інших гармонік не існує. Тому встановлені вимушені коливання маятника, які зумовлені довільною періодичною силою, можна розглядати як результат накладання встановлених вимушених коливань цього маятника, зумовлених кожною з гармонік сили. Внесок різних гармонік в загальне коливання залежить від їхніх частот і амплітуд. Завдяки явищу резонансу суттєвий внесок дають лише ті гармоніки, частоти яких наближені до резонансної частоти. Якщо коефіцієнт загасання коливань 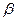малий, то маятник може здійснювати коливання, подібні до гармонічних, навіть якщо змушувальна сила не є гармонічною.