За теоремою косинусів
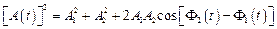 ,
,
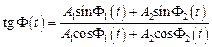 .
.
Два коливання 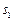 і
і 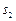 називаються когерентними, якщо різниця їхніх фаз не залежить від часу:
називаються когерентними, якщо різниця їхніх фаз не залежить від часу:
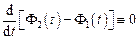 і
і 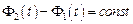 .
.
Оскільки  , то циклічні частоти когерентних коливань мають бути однакові, тобто
, то циклічні частоти когерентних коливань мають бути однакові, тобто 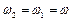 . В будь-який час різниця фаз когерентних коливань дорівнює різниці їх початкових фаз:
. В будь-який час різниця фаз когерентних коливань дорівнює різниці їх початкових фаз: 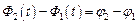 . Відповідно результуючі коливання – гармонічні з тією ж самою циклічною частотою
. Відповідно результуючі коливання – гармонічні з тією ж самою циклічною частотою 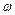 , тобто
, тобто

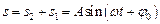 ,
,
де
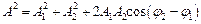 ,
, 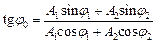 .
.
В залежності від величини різниці початкових фаз коливань, які додаються, амплітуда А результуючого коливання змінюється в межах від
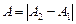 , при
, при 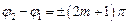
до
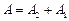 , при
, при 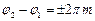 ,
,
де 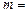 0, 1, 2, ... – довільне ціле невід’ємне число. Якщо
0, 1, 2, ... – довільне ціле невід’ємне число. Якщо 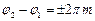 , то кажуть, що коливання синфазні (знаходяться в одній фазі), а при
, то кажуть, що коливання синфазні (знаходяться в одній фазі), а при 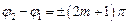 кажуть, що коливання знаходяться в протифазі.
кажуть, що коливання знаходяться в протифазі.
Гармонічні коливання, частоти яких відрізняються ( 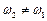 ), некогерентні, оскільки різниця їхніх фаз, яка дорівнює
), некогерентні, оскільки різниця їхніх фаз, яка дорівнює 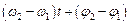 , безперервно змінюється з часом. При накладанні таких коливань виникають негармонічні результуючі коливання. Вектори амплітуд
, безперервно змінюється з часом. При накладанні таких коливань виникають негармонічні результуючі коливання. Вектори амплітуд 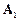 і
і 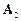 коливань, які додаються (рис.9.6), обертаються з різними кутовими швидкостями. В результаті, побудований на них паралелограм безперервно деформується, а його діагональ – вектор
коливань, які додаються (рис.9.6), обертаються з різними кутовими швидкостями. В результаті, побудований на них паралелограм безперервно деформується, а його діагональ – вектор 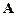 результуючих коливань – змінює довжину і обертається зі змінною кутовою швидкістю.
результуючих коливань – змінює довжину і обертається зі змінною кутовою швидкістю.
Два гармонічних коливання з різними циклічними частотами 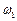 і
і 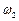 можна наближено вважати когерентними лише протягом часу
можна наближено вважати когерентними лише протягом часу  , коли їхня різниця фаз слабко змінюється:
, коли їхня різниця фаз слабко змінюється: 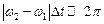 , або
, або 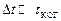 , де
, де 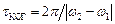 – час когерентності розглядуваних коливань.
– час когерентності розглядуваних коливань.
Негармонічні коливання, які виникають внаслідок накладання двох однаково спрямованих гармонічних коливань з близькими частотами, називаються биттям. В цьому випадку за початок відліку часу доцільно обрати момент, коли фази обох коливань 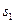 і
і 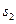 співпадають і дорівнюють
співпадають і дорівнюють 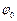 . Тоді
. Тоді  і
і 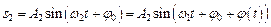 , де
, де 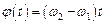 . Результуюче коливання задовольняє співвідношення
. Результуюче коливання задовольняє співвідношення
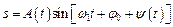 ,
,
де
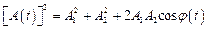 ,
, 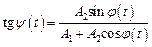 .
.
 Зокрема, якщо
Зокрема, якщо 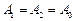 , то
, то
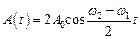 і
і
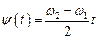 ,
,
а отже
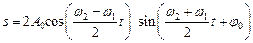 .
.
Величина 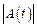 , що характеризує амплітуду коливань при битті, змінюється в межах від
, що характеризує амплітуду коливань при битті, змінюється в межах від 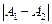 до
до 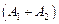 з циклічною частотою
з циклічною частотою 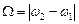 , яка називається циклічною частотою биття. Оскільки частота биттів набагато менша за частоту коливань (
, яка називається циклічною частотою биття. Оскільки частота биттів набагато менша за частоту коливань ( 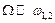 ), змінну величину
), змінну величину 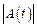 умовно називають амплітудою биття. Період биттів
умовно називають амплітудою биття. Період биттів 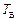 і частота биттів
і частота биттів 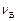 дорівнюють:
дорівнюють:
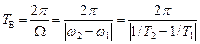 ,
,
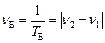 ,
,
де 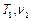 і
і 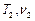 – періоди і частоти коливань, що додаються. Характер залежності s від часу t при битті наведено на рис.9.10 для випадку
– періоди і частоти коливань, що додаються. Характер залежності s від часу t при битті наведено на рис.9.10 для випадку 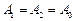 .
.
Дата добавления: 2015-04-07; просмотров: 850;
