Механічні коливання

Якщо матеріальна точка здійснює прямолінійні гармонічні коливання навколо положення рівноваги вздовж осі координат ОХ, а початок координат співпадає з точкою рівноваги, то залежність координати 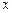точки від часу 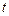має вигляд

.

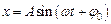Проекції швидкості 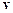та прискорення 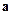точки на вісь ОХ дорівнюють:

,

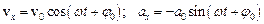де 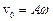– амплітуда швидкості, 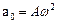– амплітуда прискорення. Звідси прискорення точки можна виразити через її зміщення як 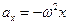. З іншого боку, згідно з другим законом Ньютона, прискорення матеріальної точки визначається силою. Отже, у випадку гармонічних коливань можна отримати

,

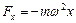тобто сила пропорційна зміщенню матеріальної точки від положення рівноваги і спрямована в протилежний бік. Цю залежність можна також представити як

,

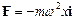де 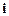– орт осі ОХ. Така залежність сили від зміщення властива пружній силі. Тому сили іншої природи, які задовольняють такий ж самий вид залежності, називаються квазіпружними силами.

Кінетична енергія матеріальної точки, яка здійснює прямолінійні гармонічні коливання, дорівнює:

.

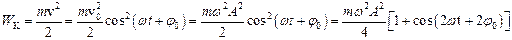Кінетична енергія матеріальної точки періодично змінюється від 0 до і при цьому здійснює гармонічні коливання з циклічною частотою і амплітудою навколо середнього значення, рівного .

Потенціальна енергія матеріальної точки, яка здійснює гармонічні коливання внаслідок дії квазіпружної сили, дорівнює:

,

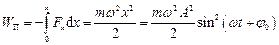або

.

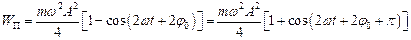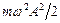Потенціальна енергія матеріальної точки періодично змінюється від 0 до і при цьому здійснює гармонічні коливання з циклічною частотою 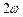і амплітудою 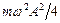навколо середнього значення, рівного 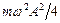. Коливання потенційної та кінетичної енергії зсунуті по фазі на 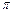, і повна енергія системи не змінюється при коливаннях:

.

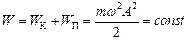Графіки залежностей 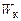, 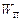і 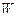від часу для випадку 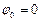наведені на рис.9.3.

Приклад 1. Лінійний гармонічний осцилятор – матеріальна точка маси m, яка здійснює прямолінійні гармонічні коливання під дією пружної сили 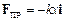. Прикладом такої системи може бути пружинний маятник – важок маси m, який закріплений на абсолютно пружній пружині ( 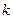– коефіцієнт, що характеризує пружні властивості пружини). За відсутності будь-яких зовнішніх сил рівняння руху має вигляд:

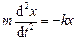або ,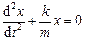

що співпадає з рівнянням гармонічних коливань. Отже, осцилятор (пружинний маятник) здійснює гармонічні коливання з частотою 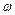і періодом 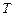, які визначаються з рівняння руху

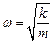і .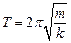

Потенціальна енергія лінійного гармонічного осцилятора

.

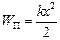Приклад 2.Пружинний маятник при наявності сталої сили.Важок маси 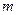вертикально підвішений на пружині жорсткістю 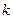у полі Земного тяжіння (рис.9.4). У рівновазі важок висить нерухомо, а пружина деформована (розтягнута) на величину 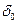. При цьому сили, прикладені до важка, скомпенсовані, тобто сила тяжіння до Землі за модулем дорівнює пружній силі, з якою пружина діє на важок, 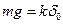. Якщо вивести важок з положення рівноваги (наприклад, відтягти його вертикально вниз на відстань 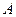від положення рівноваги і відпустити без поштовху), важок почне рухатись згідно з наступним рівнянням руху

.

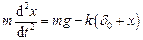Звідси отримаємо рівняння гармонічних коливань, 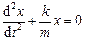, яке повністю співпадає з рівнянням, розглянутим у попередньому прикладі. Отже, стала сила не впливає на частоту коливань пружинного маятника, вона лише зміщує положення рівноваги (на величину ).

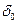Приклад 3.Послідовне з’єднання пружин маятника.

Розглянемо пружинний маятник, що складається з важеля 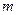, підвішеного на двох пружинах різної жорсткост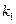і, і 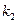(рис.9.5). Як і в попередньому прикладі будемо відраховувати зміщення важеля по відношенню до його положення рівноваги. Зміщення важеля представимо як суму 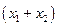, де 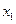- видовження першої пружини по відношенню до її довжини, що відповідає рівноважному положенню важеля, 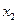- те ж саме для другої пружини. Приймемо до уваги, що при послідовному з’єднанні пружна сила однакова в обох пружинах, тобто 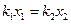. Запишемо рівняння руху

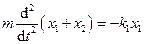, або ,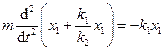

звідки отримаємо шукане рівняння гармонічних коливань

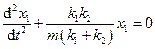
і відповідно частоту коливань

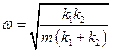
Приклад 4.Паралельне з’єднання пружин маятника (рис.9.6).

Задача принципово подібна до попередньої. Відмінність полягає в тому, що при паралельному з’єднанні видовження пружин однакові, а сили пружності різні і обидві діють на важіль. Рівняння руху має вигляд

,

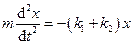звідки отримаємо

.

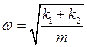Приклад 5.Фізичний маятник – тверде тіло, яке здатне коливатись під дією сили тяжіння 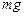навколо нерухомої горизонтальної осі О, яка не проходить через центр ваги тіла (рис.9.7) і має назву вісь обертання маятника. Центр ваги маятника співпадає з його центром інерції С. Точка О перетину осі гойдання маятника з вертикальною площиною, яка проходить через центр ваги маятника і перпендикулярна до осі гойдання, називається точкою підвісу маятника.

Для опису руху такого маятника зручно застосувати рівняння моментів у вигляді 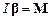. За відсутності сил тертя у точці підвісу рівняння руху маятника має вигляд

,

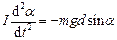де 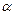– кут повороту маятника навколо осі гойдання з положення рівноваги, 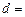ОС – відстань від центра інерції маятника до осі гойдання, 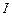– момент інерції маятника навколо цієї ж осі, 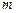– маса маятника, 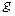– прискорення вільного падіння. При малих коливаннях маятника (малих відхиленнях від положення рівноваги) 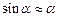і рівняння руху маятника набуде вигляду

,

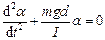тобто кут 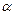задовольняє диференційне рівняння гармонічних коливань. Таким чином, за відсутності тертя малі коливання фізичного маятника є гармонічними:

,

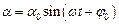де 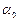– амплітуда коливання кута 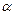, а

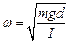і .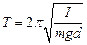

– циклічна частота і період малих коливань фізичного маятника.

Приклад 6. Математичний маятник – матеріальна точка, яка підвішена на невагомій нерозтягненій нитці і здійснює коливання у вертикальній площині під дією сили тяжіння. Математичний маятник являє собою граничний випадок фізичного маятника, уся маса якого зосереджена в центрі інерції, так що 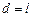– довжина математичного маятника. Момент інерції такого маятника відносно осі гойдання 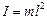. Відповідно, циклічна частота і період малих коливань математичного маятника дорівнюють:

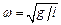і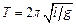

В загальному випадку період коливань фізичного маятника залежить від його амплітуди :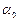

.

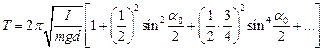Зміна величини 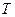при збільшенні 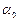до 15° не перевищує 0.5 %.

Зведеною довжиною фізичного маятника 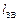називається довжина математичного маятника, що має такий самий період коливань:

,

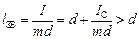де 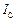– момент інерції фізичного маятника відносно осі, що проходить через центр інерції С маятника і паралельний його вісі гойдання. Точка О₁, що знаходиться на прямій ОС на відстані 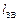від точки підвісу маятника О, називається центром гойдання фізичного маятника. Центр гойдання та точка підвісу мають властивість взаємності: якщо маятник підвісити таким чином, щоб вісь гойдання проходила через точку О₁, то точка О буде співпадати з новим положенням центра гойдання маятника, тобто зведена довжина і період коливань фізичного маятника залишаться незмінними.