Гармонічні коливання

Коливаннями називають процеси (рухи або зміни стану), які повторюються в часі. В залежності від фізичної природи коливального процесу і “механізму” його збудження розрізняють: механічні коливання (коливання маятників, струн, частин машин і механізмів, будов, мостів та ін. 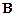споруд, тиску повітря при розповсюдженні в ньому звуку, хитання корабля, хвилювання моря і т.п.); електромагнітні (коливання змінного електричного струму в колі, коливання векторів і електричної напруженості і магнітної індукції змінного електромагнітного поля і т.д.); електромеханічні (коливання мембрани телефона, дифузора електродинамічного гучномовця і т.п.) та ін.

Система, яка здійснює коливання, називається коливальною системою. Вільними коливаннями (власними коливаннями) називаються коливання, що відбуваються за відсутності змінних зовнішніх впливів на коливальну систему і виникають внаслідок якого-небудь початкового відхилення цієї системи від стану її стійкої рівноваги. Вимушеними коливаннями називаються коливання, що виникають в системі під впливом змінного зовнішнього впливу (наприклад, коливання сили струму в електричному колі, зумовлені змінною е.р.с.; коливання маятника, зумовлені змінною зовнішньою силою).

Коливання називаються періодичними, якщо значення фізичних параметрів, які характеризують коливну систему і змінюються при коливаннях, повторюються через рівні проміжки часу. Найменший проміжок часу 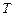, що задовольняє такій умові, називається періодом коливань. За період коливань 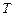система здійснює одне повне коливання. Частотою періодичних коливань називається величина 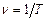, яка дорівнює кількості повних коливань, що відбуваються в одиницю часу. Циклічною, або круговою, частотою періодичних коливань називається величина 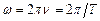, рівна кількості повних коливань, які відбуваються в 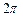одиниць часу. При періодичних коливаннях залежність коливальної величини s від часу t задовольняє умові .

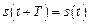Періодичні коливання величини 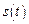називаються гармонічними коливаннями, якщо

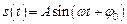або ,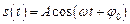

де 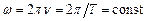– циклічна, або кругова, частота гармонічних коливань, 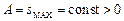– максимальна величина коливальної величини 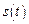, яку називають амплітудою коливань, 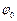– стала величина. Оскільки функції сінуса і косінуса перетворюються одна в одну при додаванні до аргумента величини 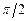, то надалі для спрощення ми будемо розглядати лише одне з вищенаведених представлень гармонічних коливань, а саме, .

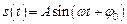Величина 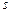в довільний момент часу 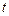визначається значенням фази коливань . Величина 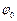є початкова фаза коливань, тобто значення 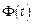в момент ( ): 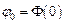. (Примітка. Момент - це початок відліку часу, а не початок коливань. Гармонічні коливання існують на інтервалі 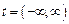. Зрозуміло, що такі коливання без початку і без кінця – це математична абстракція, модель.)

Перша та друга похідні по часу від гармонічної коливальної величини 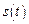також здійснюють коливання такої ж циклічної частоти:

,

,

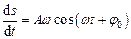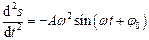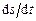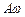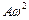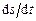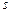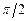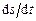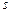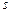причому амплітуди і відповідно дорівнюють і . Різниця фаз коливань і стала і дорівнює (це різниця фаз між коливаннями функції і функції ). Іншими словами, коливання величини випереджають за фазою коливання величини на p/2. Аналогічно, різниця фаз коливань і дорівнює 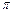(це різниця фаз між коливаннями функції і функції ). Або, випереджає 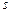за фазою на 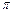. Графіки залежності від часу величин 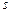, , 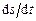при гармонічних коливаннях для випадку 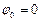наведені на рис.9.1.

Можна впевнитись, що гармонічна коливальна функція 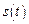задовольняє диференційне рівняння

.

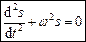Загальним розв’язком такого рівняння є наступна функція:

,

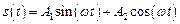де 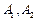– сталі інтегрування. Значення сталих 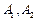можна знайти з початкових умов, тобто значень 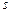і 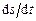в початковий момент часу ( ):

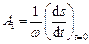і .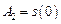

Загальний розв’язок можна привести до більш поширеного вигляду гармонічних коливань 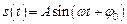, якщо застосувати перетворення

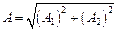і .

Таким чином, величина 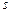здійснює гармонічні коливання лише в тому випадку, якщо вона задовольняє наведене вище диференційне рівняння, яке тому і називається диференційним рівнянням гармонічних коливань.

Гармонічні коливання можна зобразити графічно як вектор на площині. Для цього з початку координат О на площині проводять вектор 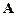(рис.9.2), модуль якого дорівнює амплітуді розглядуваних коливань і складає з віссю координат ОХ кут 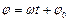, який дорівнює фазі коливань в даний момент часу 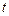. З часом кут 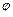збільшується так, що вектор 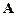рівномірно обертається навколо точки О з кутовою швидкістю, яка дорівнює циклічній частоті коливань 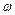. Відповідно проекція вектора 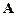на вертикальну вісь OY здійснює гармонічні коливання за законом:

.

Графічне зображення гармонічних коливань за допомогою обертального вектора амплітуди називається методом векторних діаграм. Цим методом широко користуються, наприклад, при додаванні однаково спрямованих гармонічних коливань.