Стаціонарний рух в’язкої рідини в трубі. Формула Пуазейля
При русі реальної рідини в трубі виникають особливості, зумовлені наявністю сил внутрішнього тертя. Зокрема, швидкість руху рідини поблизу стінок труби дорівнюватиме нулеві, і буде максимальною в центрі труби. Для циліндричної труби можна довести, що швидкість течії змінюється вздовж радіуса за таким законом:

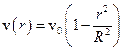 ,
,
де 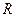 – радіус труби,
– радіус труби, 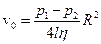 – швидкість руху рідини на осі труби (максимальна швидкість),
– швидкість руху рідини на осі труби (максимальна швидкість), 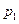 і
і 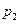 – величини тисків на вході і на виході з труби,
– величини тисків на вході і на виході з труби, 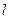 – довжина труби. Графік залежності швидкості v від радіуса r наведено на рис.8.20.
– довжина труби. Графік залежності швидкості v від радіуса r наведено на рис.8.20.
Потік рідини 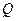 , тобто об’єм, який проходить через поперечний переріз труби в одиницю часу, дорівнює:
, тобто об’єм, який проходить через поперечний переріз труби в одиницю часу, дорівнює:
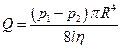 .
.
Ця формула називається формулою Пуазейля. Вона дозволяє експериментально визначати в’язкість рідин шляхом вимірювання об’єму рідини, який проходить в одиницю часу через трубу з заданими радіусом 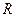 та довжиною
та довжиною 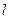 .
.
Маса рідини, яка проходить в одиницю часу через поперечний переріз труби, дорівнює 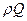 , а кінетична енергія, що переноситься через поперечний переріз в одиницю часу:
, а кінетична енергія, що переноситься через поперечний переріз в одиницю часу:
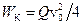 .
.
Робота, яка виконується над рідиною різницею тисків 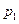 і
і 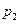 , є:
, є:
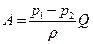 .
.
Таку ж саму роботу, але протилежну за знаком, виконують сили в’язкості, оскільки при стаціонарному русі кінетична енергія рідини залишається незмінною:
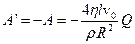 .
.
При розгляді руху рідини в трубах можна знехтувати в’язкістю та користуватись рівнянням Бернуллі, коли 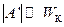 , тобто
, тобто
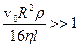 .
.
Дата добавления: 2015-04-07; просмотров: 1536;
