Атмосфера в полі тяжіння. Барометрична формула

Тиск повітря поблизу поверхні Землі зумовлений його власною вагою і складає приблизно 10⁵ Па, тобто на 1 м² поверхні Землі повітря тисне з силою 10⁵ H. Такий тиск називають атмосферним. Він зменшується при збільшенні відстані від поверхні Землі. Проте, залежність тиску від висоти є нелінійною. Такий факт пояснюється тим, що густина атмосфери є змінною. Тобто атмосферне середовище (повітря) є стисливим.

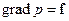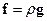Отримаємо закон, за яким зменшується тиск атмосфери при зростанні відстані від поверхні Землі. Скористаємося основним рівнянням гідростатики, а саме , де . Вісь z спрямуємо вгору, перпендикулярно до поверхні Землі. Тоді основне рівняння гідростатики набуде вигляду:

.

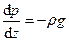Тиск 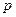, густина 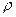і температура 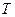повітря зв’язані між собою рівнянням стану. Якщо густина газу не дуже велика (газ можна вважати ідеальним), то стан газу маси 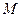описується рівнянням Клапейрона:

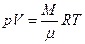, або ,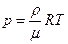

де 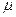– молярна маса газу, R – газова стала.

Рівняння Клапейрона робить можливим виключити з основного рівняння гідростатики густину. В результаті отримаємо:

.

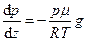Скористаємося певною ідеалізацією. Зокрема, будемо вважати, що атмосфера є ізотермічною. Атмосфера називається ізотермічною, якщо вона знаходиться в механічній і тепловій (термодинамічній) рівновазі. Механічною рівновагою називають такий стан атмосфери, при якому вона залишається нерухомою з часом, тобто в атмосфері відсутні повітряні потоки (вітри і т.п.). Теплова рівновага означає, що температура Т є однаковою в будь-якій точці атмосфери: 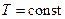. Очевидно, що ізотермічна атмосфера є ідеалізацією. В такому наближенні отримане рівняння легко інтегрується:

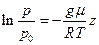, або ,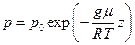

де 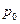– величина атмосферного тиску на поверхні Землі.

За аналогічним законом змінюється і густина повітря:

,

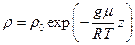де 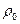– густина атмосфери на поверхні Землі.

Отримані співвідношення називається барометричними формулами.

Численні дослідження атмосфери показують, що при збільшенні висоти тиск і густина монотонно зменшуються, а температура змінюється за більш складним законом. Нагадаємо, що барометричні формули отримані в наближенні, що температура не змінюється з висотою. Для того, щоб врахувати таку зміну і отримати більш коректну залежність тиску від висоти, слід в рівняння 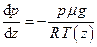підставити реальну залежність 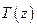. Розв’язок такої задачі є досить складним і тому ми лише обмежимося якісним розглядом процесів, що відбуваються в реальній атмосфері.

Так, лише в нижньому 10-кілометровому шарі температура монотонно зростає при збільшенні висоти від поверхні Землі, а в більш високих шарах залежність є немонотонною. Складна висотна залежність температури атмосфери є результат спільного прояву зумовлених сонячним випромінюванням процесів переносу тепла і повітряних мас. Земля за відсутності атмосфери нагрілася б на екваторі до 270 К, на Південному полюсі – до 150 К і на Північному полюсі – до 170 К. При таких температурах встановилася б радіаційна рівновага: нагріта Земля випромінювала б у світовий простір стільки ж енергії, скільки одержувала від Сонця. Проте, поверхня Землі значно тепліша, а різниця температур між екватором і полюсом набагато менша. Це є результатом поглинання сонячної енергії самою атмосферою. Крім того, атмосфера й океан переносять тепло від однієї області до іншої, що також впливає на енергетичний баланс.

Поглинання сонячної енергії здійснюється головним чином водяною парою, вуглекислим газом і озоном, унаслідок чого створюється “парниковий ефект”, який приводить до додаткового нагрівання поверхні Землі. Повітря поблизу поверхні є більш теплим і легким, ніж повітря у верхніх шарах. Тому відбувається вертикальна конвекція – нижні шари атмосфери піднімаються догори і перемішуються з масами повітря верхніх шарів. Тому на практиці реалізується складний розподіл температури, який є результатом динамічної рівноваги атмосфери в полі сили тяжіння та дотримання балансу енергії.

Атмосфера поділяється на окремі ділянки. Нижній шар атмосфери, який називається тропосферою, містить 80% маси атмосфери, майже всю водяну пару і характеризується сильним вертикальним перемішуванням. Зверху тропосфера обмежена тропопаузою, де температура атмосфери змінюється дуже слабко. Вище розташована стратосфера, у якій повітряні маси перемішується слабко. Зростання температури закінчується в стратопаузі. Вище знаходиться мезосфера, де температура спадає. Мезосфера містить лише 0.1% маси всієї атмосфери. Вище мезосферы (h>100 км) знаходиться термосфера, де температура знову зростає при збільшенні висоти від поверхні Землі і сягає 600 К в період спокійного Сонця і більш 2000 К в період сонячної активності.

Відзначені вертикальні перемішування повітряних мас атмосфери є проявом її механічної нестійкості. Проаналізуємо більш детально фізичну природу такого процесу. Розглянемо порушення стану механічної рівноваги, коли певна маса повітря трохи піднімається догори. В новому її положенні ця повітряна маса буде зазнавати меншого зовнішнього тиску, що зумовить її розширення, і, відповідно, зменшення її густини. Це відбудеться внаслідок того, що при малій теплопровідності повітря за час руху догори розглядувана маса практично не буде обмінюватись теплом з оточенням. Якщо виявиться, що в новому положенні густина повітряної маси, які піднялася, буде більшою за густину навколишнього повітря, то ця маса за законом Архімеда буде рухатись донизу, і рівновага відновиться. Якщо ж її густина виявиться меншою за густину навколишнього повітря, то вона буде підніматися ще вище, і механічна рівновага виявиться нестійкою. Буде відбуватись вертикальний переніс повітряної маси. Аналогічні міркування справедливі і для випадку, коли порушення механічної рівноваги відбувається шляхом невеликого зниження певної маси повітря.

Дослідження атмосфери Землі показали, що ізотермічна атмосфера в розглядуваному контексті є стійкою. Ще більша стабільність атмосфери має місце, коли температура повітря зростає з висотою. Якщо ж температура зменшується при збільшенні висоти, то механічна рівновага повітря можлива лише тоді, коли ця зміна не є дуже швидкою. Так, при зменшенні температури з висотою більш ніж на один градус на кожні 100 метрів висоти атмосфера втрачає механічну стійкість – з'являються вертикальні потоки повітряних мас, які називаються конвекцією.

Гравітаційне самостиснення планети

Неважко уявити, що в результаті гравітаційної взаємодії між різними частинами планети виникають сили притягання, що призводить до виникнення додаткового тиску всередині планети. Знайдемо цей тиск.

Нехай планета являє собою однорідну кулю радіуса 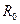маси 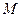. Застосуємо основне рівняння гідростатики

.

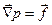Щоб записати вираз для об’ємної густини гравітаційних сил, згадаємо, що сила тяжіння всередині планети пропорційна відстані до її центра, тобто 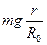. Звідси очевидно, що густина сил тяжіння всередині планети може бути представлена виразом

,

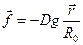де 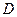- густина, 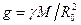- прискорення вільного падіння на поверхні планети.

Запишемо векторне основне рівняння гідростатики у вигляді системи рівнянь:

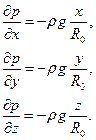
Повний диференціал тиску можна записати як

.

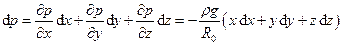Проінтегруємо отримане диференційне рівняння

.

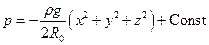Сталу інтегрування знайдемо з такої очевидної граничної умови: на поверхні планети тиск дорівнює нулю, а сума квадратів координат дорівнює квадрату її радіуса, тобто 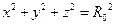. Тод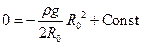і , і 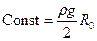. Врахуємо також 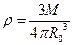і запишемо вираз для тиску гравітаційного самостиснення:

.

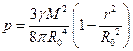Таким чином, з наближенням до центру планети тиск збільшується за квадратичним законом і в центрі планети ( 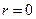) досягає величини

.

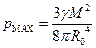Якщо у цю формулу підставити чисельні значення параметрів Землі, отримаємо 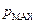близька 1.8×10⁶ атм (1 атм»10⁵ Па). При цьому слід відзначити, розглянута задача лише віддалено відповідає реальній ситуації для Землі. На початку розгляду було зроблено припущення про однорідність розглядуваної планети. Нашу Землю можна лише наближено вважати однорідною, оскільки експерименти свідчать про суттєве зростання густини з глибиною.

Гідростатична модель обертання планети

Розглянемо ізольовану кулю маси 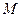з нестисненої рідини густиною 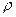, яка обертається навколо власної осі з кутовою швидкістю 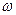. Оберемо Декартову систему координат, яка обертається разом з планетою, причому початок координат знаходиться у центрі планети. Вісь OZ спрямуємо уздовж осі обертання. Радіус планети позначимо .

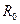Розглянемо елемент об’єму 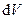, який знаходиться на відстані 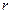від центру планети (рис.8.5). На обраний елемент діє сила тяжіння, яка спрямована до центру планети і дорівнює 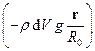, де 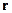- радіус-вектор обраного елемента об’єму. Отже, вектор об’ємної густини гравітаційних сил може бути представлений як .

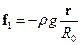Оскільки обрана система відліку неінерційна, то на обраний елемент діє відцентрова сила інерції, яка дорівнює 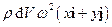. Відповідний вектор густини сил інерції .

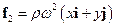Запишемо основне рівняння гідростатики у проекціях на вісі координат:

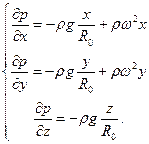
Звідси повний диференціал тиску можна записати як

.

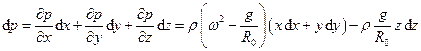Проінтегруємо отримане диференційне рівняння

.

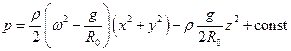Скористаємось тією обставиною, що отриманий вираз дозволяє розрахувати тиск у будь-якій точці. Оскільки тиск на поверхні планети повинен бути скрізь однаковим, прирівняємо значення 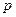на полюсі, 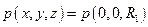, і на екваторі, 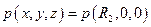. При цьому ми змушені припустити, що полярний і екваторіальний радіуси планети різні:

,

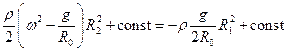де 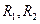- відповідно полярний та екваторіальний радіуси планети. Звідси

.

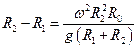Оскільки очікується, що різниця радіусів буде невеликою, наближено покладемо 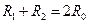. Тоді отримаємо відносну величину зміни радіуса

,

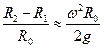яка характеризує ступінь сплюснутості планети, що зумовлена її обертанням навколо власної вісі. Якщо в отриману формулу підставити параметри Землі, отримаємо величину 0.0016, яка лише приблизно вдвічі відрізняється від відомої реальної величини сплюснутості Землі. Отримана узгодженість розрахункової величини з реальною свідчить про те, що Земля знаходиться у стані, близькому до гідростатичної рівноваги.