Стаціонарний рух ідеальної рідини. Рівняння Бернуллі

8.8.1. Вивчення руху реальних рідин є досить складною задачею. Для її спрощення користуються поняттям ідеальної рідини. Рідина, у якій при будь-яких рухах не виникають сили в’язкості (сили тертя), називається ідеальною. Розглянемо стаціонарний рух ідеальної рідини в полі тяжіння і застосуємо до неї закон збереження енергії. 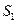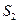Нехай ідеальна рідина рухається в трубці струму, поперечний переріз якої змінюється від до (рис.8.9), в напрямку зліва направо. Відокремимо в трубці малий стовпчик ABCD і розглянемо роботу, яку виконують сили тиску при його переміщенні в нове положення A’B’C’D’.

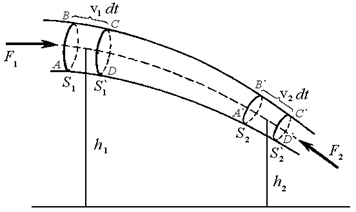
Рис.8.9.

Так, на переріз AB стовпчика рідини діє сила 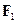, а на переріз CD – сила 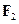. Відзначимо, що сили тиску, які діють на бокову поверхню трубки, перпендикулярні напрямку руху і тому роботи не виконують. Через малий проміжок часу 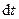переріз 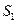переміститься на відстань 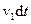у положення 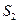, а переріз 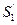на відстань 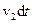у положення 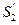. При цьому, сили, що діють на рідину в трубці, виконують роботу:

.

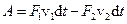Оскільки тертя відсутнє, то ця робота має дорівнювати приросту енергії розглядуваного об’єму рідини. Можна уявити собі, що маса 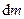рідини між перерізами 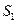і 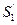зникає, і така ж сама маса 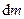з’являється між перерізами 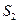і 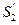. Кінетична та потенційна енергії стовпчика рідини ABCD дорівнюють відповідно:

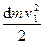і ,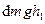

а стовпчика A’B’C’D’:

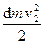і ,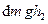

де 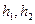– висоти відповідних об’ємів рідини над певним умовно обраним горизонтальним рівнем.

Таким чином, запишемо умову рівності роботи А приросту повної енергії:

.

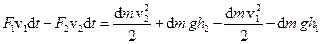Сили 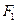і 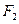, обумовлені тиском рідини на розглядувані об’єми рідини, можна представити наступним чином:

.

Якщо підставити ці співвідношення у наведене вище рівняння і врахувати, що 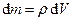, де 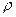– густина рідини, 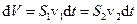– об’єм, то за допомогою нескладних перетворень отримаємо:

.

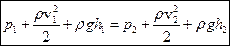Таке рівняння було вперше отримано Бернуллі і, відповідно, називається рівнянням Бернуллі. Відзначимо, що виведення рівняння Бернуллі проведено для окремої трубки струму, проте воно справедливе для всього потоку рідини.

8.8.2. Далі розглянемо окремі випадки практичного застосування рівняння Бернуллі.

Для трубки струму, що розміщена горизонтально ( 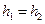) рівняння Бернуллі є наступним:

.

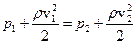З отриманого рівняння та теореми нерозривності випливає, що при русі рідини в трубі, що має різні площі поперечного перерізу, швидкість буде більшою у вужчих місцях, а тиск буде більшим в більш широких місцях. Це можна показати на досліді, якщо встановити вздовж труби кілька манометричних трубок (рис.8.10). Висота рідини в цих трубках показує величину тиску. Дослід підтверджує отриманий наслідок з закону Бернуллі. А саме, в манометричній трубці b, що знаходиться у вужчій частині труби, рівень рідини нижчий, ніж у трубках a і c, що вимірюють тиск в частинах труби з більшим поперечним перетином.

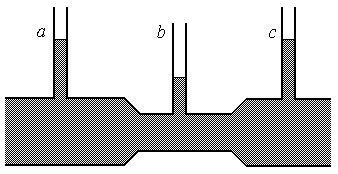
Рис.8.10.

Наведена особливість течії рідини на практиці використовується у приладах для вимірювання витрат води (лічильниках води). В основу цих приладів покладена труба зі змінним поперечним перерізом (труба Вентурі), яка оснащена манометрами для вимірювання тисків 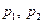у перерізах 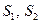. Витрата води (маса, що протікає в одиницю часу) визначається рівністю

,

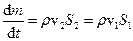яка, разом з рівнянням Бернуллі, утворюють систему рівнянь для знаходження витрат води. З врахуванням того, що тиски 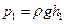і 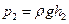визначаються з показань 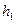і 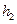манометричних трубок, отримаємо:

.

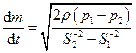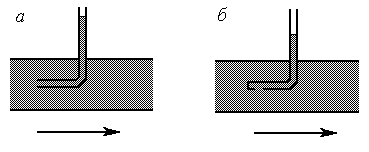
Рис. 8.11.

8.8.3. Зупинимося більш детально на питанні вимірювання тисків в рідині, що рухається. Якщо в потік рідини помістити трубку, нижній кінець якої зігнений в напрямку, протилежному потоку (рис.8.11,а) – трубку Піто, то лінії струму зміняться поблизу неї. Швидкість руху рідини перед отвором буде дорівнювати нулеві. Рівняння Бернуллі в такому випадку набуде вигляду: ,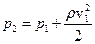

де 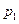– тиск в рідині, який би виміряв манометр у випадку його руху разом з рідиною. Манометр, приєднаний до трубки Піто виміряє тиск 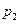, який на 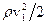більший за тиск 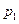. Доданок 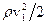називається “динамічним тиском”. Якщо ж в тонкій трубці зробити отвір в бічній поверхні вигнутої частини, то поблизу нього швидкість і тиск будуть мало відрізнятись від відповідних величин за відсутності трубки. Тому такий прилад (рис.8.11,б) називають зондом. Приєднання манометра до зонду дасть можливість виміряти тиск рідини 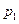,який існує в місці знаходження отвору. Тиск 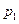часто називають статичним тиском, щоб підкреслити його відмінність від динамічного. Сума динамічного та статичного тиску і називається повним тиском .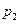

Якщо відомі динамічний та статичний тиски, то можна визначити швидкість руху рідини 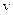. Такий принцип реалізовано в трубці Прандтля, яка поєднує зонд і трубку Піто (рис. 8.12). Якщо їх приєднати до диференційного манометра (манометра, який вимірює різницю тисків), то він покаже величину динамічного тиску 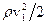. Це в свою чергу дозволить визначити швидкість рідини, якщо відома її густина.

8.8.4. Відомо, що літак В-52 має вісім двигунів, які створюють загальну силу тяги близько 8×7.7=61.6 тонн (приблизно 6×10⁵ Н). У той же час вага літака становить більше 220 тонн, що у 3.5 рази більше сумарної сили тяги. Що ж утримує літак у польоті?

Рівняння Бернуллі дозволяє пояснити механізм виникнення підйомної сили крила літака. На рис..8.13 наведено ідеалізовану картину обтікання крила літака струменями повітря. Оскільки переріз крила несиметричний (крило має вигин вгору), трубки струму звужуються над крилом, і в той же час практично не змінюються під ним. Звуження трубки струму призводить до збільшення швидкості потоку в ній і відповідно до зменшення статичного тиску над крилом. Так виникає підйомна сила 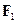, яка утримує літак в повітрі. Крім підйомної сили, на крило з боку набігаючого потоку повітря діє також сила опору 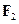, яку долають двигуни літака. Слід також відзначити, що наведене пояснення є спрощеним і не враховує багатьох важливих факторів, наприклад, явище відриву потоку.