Сили в’язкості

Поняття ідеальна рідини, рух якої ми і розглядали в попередніх розділах, є наближенням. Реальним рідинам властива в’язкість або внутрішнє тертя. Так, в реальних рідинах при переміщенні одних шарів середовища відносно інших виникають сили тертя. З боку шару, який рухається більш швидко, на шар, що рухається повільніше, діє прискорювальна сила. Навпаки, з боку шару, що рухається повільніше, на більш швидкий шар діє гальмівна сила. Ці сили називаються силами внутрішнього тертя або силами в’язкості. Напрямок їх дії спрямований по дотичній до поверхні прошарків. Величина сили внутрішнього тертя тим більша, чим більша площа 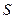поверхні розглядуваного шару і залежить від того, наскільки сильно відрізняються швидкості руху рідини у сусідніх шарах. В’язкість зумовлює те, що будь-який рух в рідині або газі поступово зникає після зникнення причин, що його спричинював. Переконатися в існуванні сил внутрішнього тертя можна на таких дослідах.

Якщо посудину з водою почати обертати навколо своєї осі зі сталою кутовою швидкістю, то рідина почне поступово обертатися. Спочатку почнуть обертатися шари, прилеглі до стінок посудини, і поступово почнуть залучатись більш віддалені шари доти, поки вся рідина не почне рівномірно обертатись. Такий результат можна пояснити лише наявністю сил взаємодії між стінками посудини і рідиною, а також між сусідніми шарами в самій рідині, що обертаються з різною кутовою швидкістю.

Іншим проявом існування сил тертя в рідинах є поступове зменшення швидкості рідини при її русі вздовж горизонтальної площини. Рівняння Бернуллі, отримане в наближенні ідеальної рідини, не передбачає такого ефекту. Внаслідок тертя частина кінетичної енергії рідини втратиться на подолання опору її руху – перейде в тепло. З цієї ж причини потік рідини, який витікає з отвору посудини, при його спрямуванні догори не підніметься до рівня води в посудині. Хоча за відсутності сил тертя це мало б мати місце – таким є результат застосування рівняння Бернуллі.

Отримати основні закони в’язкості і показати основні їх закономірності можна на такому досліді. Розглянемо дві пластинки, між якими знаходиться тонкий шар рідини (рис.8.18). Для того, щоб верхня пластинка 1 рухалась відносно нижньої зі швидкістю 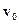, необхідно прикласти постійну силу 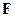в напрямку її руху. Оскільки під дією цієї сили пластина не прискорюється, то має існувати ще якась сила, яка її врівноважує. Такою силою є сила тертя, яка виникає при відносному русі пластини і рідини. Внаслідок дії сил тертя на нижню пластинку 2 діє така ж сила 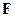. Отже, щоб залишити пластинку 2 нерухомою, до неї треба прикласти силу 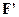. Взаємодія між пластинками зумовлена силами тертя (в’язкості), які виникають між пластинами та рідиною, і різними шарами рідини. З експерименту встановлено, що модуль сили внутрішнього тертя пропорційний швидкості 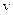, площі пластинки 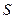і обернено пропорційний відстані між пластинками :

,

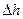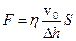де 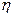– коефіцієнт в’язкості. Коефіцієнт в’язкості не залежить від матеріалу пластинок і визначається властивостями рідини. Зокрема, 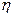зменшується при збільшенні температури рідини.

Отриману формулу можна поширити на випадок, коли обидві пластинки рухаються. Якщо швидкість першої пластинки 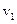, а 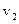– швидкість другої, то сила внутрішнього тертя дорівнюватиме:

,

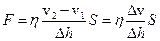або в більш загальному випадку:

,

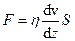де 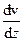– модуль градієнта швидкості, тобто величина, що показує наскільки сильно змінюється швидкість в напрямку, перпендикулярному до напрямку руху. Остання формула використовується для визначення сили тертя між будь-якими шарами.