Вимірювання в’язкості методом Пуазейля

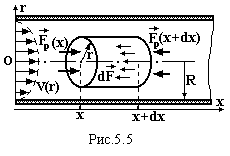
Даний метод оснований на вимірюванні витрати рідини (газу) при протіканні їх по круглій трубі. Витрата - це маса речовини, яка протікає через трубу за одиницю часу. Для її розрахунку знайдемо спочатку закон розподілу швидкості руху речовини по перерізові труби, так як вона в різних точках перерізу різна. Дійсно, біля стінок швидкість дорівнює нулю і зростає до центру перерізу.

Розглянемо в потоці рідини (газу) елементарний об’єм у формі циліндра радіусом r і довжиною dx, вісь якого співпадає з віссю труби (рис.5.5). Він рухається під дією сил тиску, що діють на основи 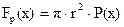і 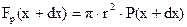, а також сила внутрішнього тертя, яка діє по бічній поверхні 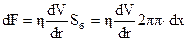. Стаціонарний рух цього елементу буде при умові 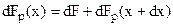, тобто

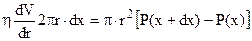, або 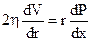. (5.7)

У випадку стаціонарного режиму течії падіння тиску на одиниці довжини труби 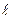є величиною сталою і дорівнює ,

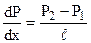де Р₁ і Р₂ – тиск на вході і на виході труби відповідно, 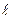- довжина труби. Рівняння (5.7) набуде вигляду

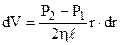. Після інтегрування 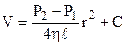. Константу інтегрування знайдемо із граничної умови: при r = R V = 0. Одержимо 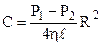. Тоді розподіл швидкості по перерізу труби як функція радіуса r буде мати вид

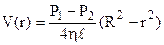(5.8)

квадратної параболи (див. рис.5.5).

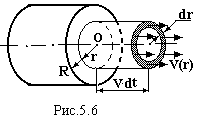Знайдемо витрату рідини. Виберемо в перерізі труби кільце радіусом r і шириною dr (рис.5.6, заштриховано). Вісь труби співпадає з центром цього кільця. Тому швидкість руху рідини по всій площі кільця однакова і задається виразом (5.8). Об’єм рідини, який пройде через це кільце за час dt, буде мати форму трубки довжиною V∙dt радіусом r і товщиною стінки dr. За цей час протече маса рідини

dm = ρ∙V∙dt∙2πr∙dr.

Тоді витрата рідини через вибране кільце буде дорівнювати 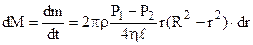. Через увесь переріз витрата знаходиться шляхом інтегрування по радіусу в межах від 0 до R

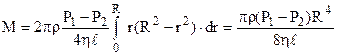. (5.9)

Звернемо увагу на досить сильну залежність витрати від радіуса труби М ~ R⁴.

Таким чином, знаючи густину рідини і вимірявши експериментально витрату М, тиски Р₁, Р₂ та геометричні розміри R і 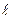, знаходять в’язкість

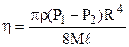. (5.10)

5.4 Ламінарний та турбулентний режими течії рідин (газів)

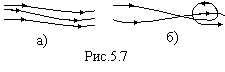Є два режими течії рідини (газу): ламінарний і турбулентний. При ламінарному режимі лінії току на перетинаються (рис.5.7,а) і шари рідини (газу) не перемішуються. При турбулентному режимі шари перемішуються, а лінії току перетинаються як між собою, так і самі себе (рис.5.7,б).

Англійський фізик О. Рейнольдс ввів безрозмірний критерій режиму течії (число Рейнольдса)

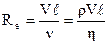, (5.11)

де V – швидкість течії, ℓ - характерний поперечний розмір труби (діаметр для круглих труб, діагональ для прямокутних), ν – кінематична в’язкість - 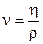, η – коефіцієнт в’язкості, ρ – густина.

При R_е < 1 режим ламінарний, при R_е > 1 – турбулентний. Слід зауважити, що це не строгий критерій, наприклад, значення R_е = 1,1 ще не означає, що режим течії турбулентний. Потрібні додаткові дослідження. Але при значенні R_е = 2 можна бути впевненим, що режим течії турбулентний.

При русі тіл в рідинах і в газах на них діють дві сили: 1) сила лобового опору F_л.о. направлена проти швидкості; 2) підіймальна сила перпендикулярна до швидкості руху.

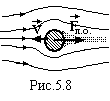
При малих швидкостях сила лобового опору зумовлена в основному силами внутрішнього тертя. При великих швидкостях (точніше при великих числах Рейнольдса) переважну роль грає різниця тисків. Попереду тіла тиск більший, ніж позаду (утворюється розрідження) (рис.5.8). Різниця сил тиску направлена проти швидкості.

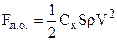Сила лобового опору , (5.12)

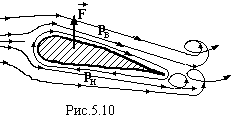
де S – максимальна площа перерізу тіла площиною, перпендикулярною до вектора швидкості 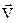, С_х – коефіцієнт лобового опору, величина стала і залежить від форми тіла і напрямку руху (рис.5.9).

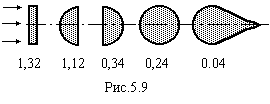З’ясуємо природу виникнення підіймальної сили крила літака. Профіль крила роблять асиметричним. Тому швидкість потоку повітря над крилом більша, ніж під ним. Крім того за крилом виникає завихрення повітря з напрямком обертання проти годинникової стрілки (рис.5.10). Ці вихрі відносять певний момент імпульсу. У відповідності з законом збереження моменту імпульсу, навколо крила утворюється циркуляційний потік протилежного напрямку обертання (по годинниковій стрілці). Він утворюється із-за наявності сил в’язкості повітря. Цей циркуляційний потік накладається на основний. Швидкість потоку над крилом зростає, а під ним – зменшується. Згідно з рівнянням Бернуллі (5.6) тиск Р_В над крилом буде менший, ніж тиск Р_Н під ним. Різниця тисків і призводить до виникненні підіймальної сили, направленої вгору (точніше в сторону, де швидкість потоку більша).

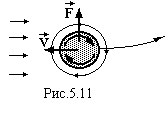Аналогічно пояснюється і ефект Магнуса (рис.5.11), який заключається у відхиленні від прямолінійного рух тіла приведеного в обертання. Тіло відхиляється в сторону де основний і циркуляційний потоки співпадають за напрямком.