I. Преобразование координат методом поворота координатных осей (определение направляющих косинусов).
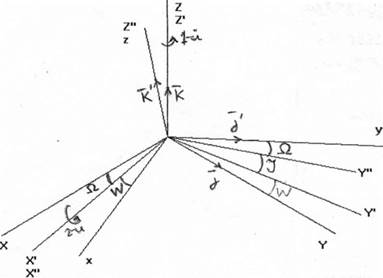
Задача:от системы координат X, Y, Z перейти к x, y, z. Решается методом поворота координатных осей.
|
1-й поворот вокруг оси OZ на угол Ω- угол прецессии
2-й поворот вокруг оси OX’ на угол нутации – I
3-й поворот вокруг оси OZ” на угол чистого вращения – W
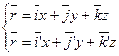
Умножим второе уравнение этой системы скалярно на векторы 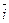 ,
, 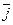 ,
, 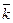 .
.
1,Космич. Геодезия(определения)
2,Задачи косм. геодезии
Тогда координаты точки будут определяться следующими формулами:
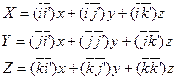
Произведение векторов является cos соответствующей стороны:
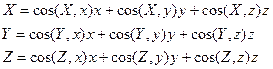
Необходимо вывести формулы направляющих косинусов:
Табл.1
| x | y | Z | |
| X | l1 | l2 | l3 |
| Y | m1 | m2 | m3 |
| Z | n1 | n2 | n3 |
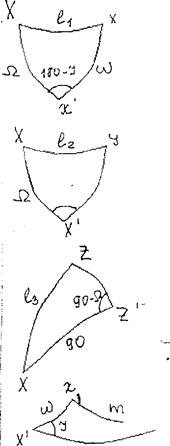
Для вывода формул воспользуемся следующим соображением: при пересечении прямоугольной системы координат со сферой образуются треугольники, у которых все стороны и углы равны 90˚.
Используя формулу cos стороны сферического треугольника:
cosa=cosb∙cosc+sinb∙sinc∙cosA
l1=cosW∙cosΩ+sinW∙sinΩ∙cos(180˚-I)
l1=cosW∙cosΩ-sinW∙sinΩ∙cosI
l2=cosΩ∙cos(90˚+W)-sinΩ∙sin(90˚+W) ∙cos(180˚-I)
l2=cosΩ∙ (-sinW)-sinΩ∙cosW∙cosI
l3=cosΩ∙cos90˚+sinΩ∙sin90∙cos(90˚-I)
l3=sinΩ∙sinI
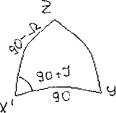
m1=cosW∙cos(90˚-Ω)+sinW∙sin(90˚-Ω) ∙cosI
m1=cosW∙sinΩ+sinW∙cosΩ∙cosI
m2=cos(90˚+W) ∙cos(90˚-Ω)+sin(90˚+W) ∙sin(90˚-Ω) ∙cosI
m2=-sinW∙sinΩ+cosW∙cosΩ∙cosI
m3=cos90˚∙cosI+sin90˚∙sinI∙cos(180˚-Ω)
m3=-sinI∙cosΩ
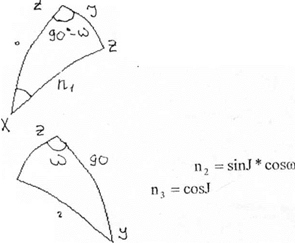
n1=cos90˚∙cosI+sin90˚∙sinI∙cos(90˚-W)
n1=sinI∙sinW
n2=cosI∙cos90˚+sinI∙sin90˚∙cosW
n2=sinI∙cosW
n3=cosI
3.Классификация системы координат
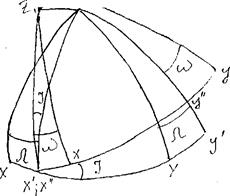
Используя формулу cos а = cos Ъ * cose + sin b * sine * cos 4 получим следующие формулы:
l1= cosΩ * cosco - sinΩ * sinw * cos J
n₁ = sinJ*sinw
m₁ = cosw * sinΩ + sinw * cosΩ* cosJ
l2 = -cosΩ * sinw - sinΩ * cosw * cosJ
n₂ = sinJ*cosw
m2 = -sinw * sinΩ + cosΩ * cosw * cosJ
l3 = sinJ*sinΩ
n₃ = cosJ
m3 = - cosΩ * sinJ
|
 |
Исходные данные:
Табл.2
| град | Мин | сек | |
| I | 22,24 | ||
| Ω | 46,18 | ||
| ω | 45,71 |
I=43˚37΄22.24˝+10΄∙№вар.
Ω=32˚15΄46,18˝-5΄∙№вар.
W=67˚23΄45,71˝+2΄№вар.
Решение
Табл.3
| sin | cos | ||
| J | 0,710671995 | 0,703524 | |
| Ω | 0,52121164 | 0,853427 | |
| w | 0,925176786 | 0,379536 | |
| l1 | -0,01534129 | ||
| l2 | -0,928741457 | ||
| l3 | 0,370410516 | 1,0 | 0,0 |
| m1 | 0,753300759 | ||
| m2 | -0,254336847 | ||
| m3 | -0,606506994 | 1,0 | 0,0 |
| n1 | 0,657497233 | ||
| n2 | 0,269725923 | ||
| n3 | 0,7035235 | 1,0 | 0,0 |
Контроль:
l12+l22+l32=1
m12+m22+m32=1
n12+n22+n32=1
∑limi=∑lini=∑mini=0
Дата добавления: 2015-06-10; просмотров: 5491;
