VII. Вычисление невозмущенной эфемериды ИСЗ.
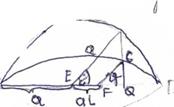
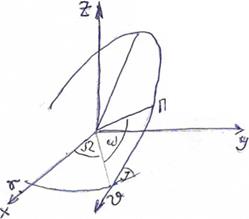
Табл.11
| исходные данные | |||||
| Xp= | 3244476,592 | a= | T= | 3h44m27.85s | |
| Yp= | 2912698,984 | e= | 0,05 | μ= | |
| Zp= | 4640189,223 | t= | 17h32m36.57s | ||
| t-T | 13,8024222 | 207,036333m | |||
| j | 2,2’’ | ||||
| Ω | 1,9’’ | ||||
| w | 1,5’’ |
- Находим среднюю аномалию М. Средняя аномалия – дуга окружности, которую описал бы ИСЗ после прохождения через перигей, если бы двигался равномерно по круговой орбите, совершая полный оборот за свой фактический период обращения по эллиптической орбите.
Е – эксцентрическая аномалия;
Υ – истинная аномалия – угол между радиус-вектором спутника и линией апсид.
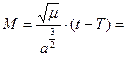 50˚46΄23,85˝
50˚46΄23,85˝
- Находим истинную аномалию (υ):
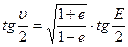 ,
,
Где Е=e∙sinE + М = 50˚49΄23,82˝
Задача решается методом приближений:
EI=M+e*sinM = 50˚46΄26,99˝
EII=e*sinEI+M = 50˚49΄23,82˝
EIII= e*sinEII+M = 50˚49΄23,82˝
EIV= e*sinEIII+M = 50˚49΄23,82˝
- Находим аргумент широты
U= υ+ω = 57˚14΄4.72˝
- Вычисляем геоцентрический радиус-вектор ИСЗ
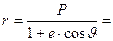 6683,292км
6683,292км
P = a∙(1-e2) = 7017,4125
r = a∙(1-e∙cosE) = 6683,292 км -контроль
- Находим геоцентрические прямоугольные координаты ИСЗ
X = (cosU∙cosΩ - sinU∙sinΩ∙cosJ) = 4826338,839
Y = (cosU∙sinΩ + sinU∙cosΩ∙cosJ) = 7499117,942
Z = sinU∙sinJ=79,98437526
Контроль: r2=X2+Y2+Z2 = 8917977,153
- Определяем прямоугольные топоцентрические координаты ИСЗ
X’=X-Xp= 4586418,958 м
Y’=Y-Yp= 1581862,247м
Z’=Z-Zp= -4640109,239 м
- Определяем топоцентрические сферические координаты и топоцентрический радиус-вектор ИСЗ.
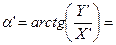 19h01m45.79s
19h01m45.79s
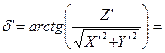 -43˚43΄25.93˝
-43˚43΄25.93˝
r’ = 8917977,153 м
Дата добавления: 2015-06-10; просмотров: 2877;
