V. Вычисление сферических экваториальных геоцентрических координат спутника по данным его топоцентрическим координатам.
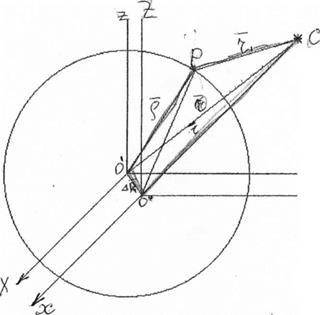
O’P= p –радиус-вектор пункта Р относительно центра референц-эллипсоида;
OP=ρ – радиус-вектор пункта Р относительно центра масс Земли;
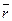 - радиус-вектор спутника относительно центра масс Земли;
- радиус-вектор спутника относительно центра масс Земли;
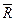 -радиус-вектор спутника относительно центра масс Земли;
-радиус-вектор спутника относительно центра масс Земли;
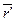 - топоцентрический радиус-вектор спутника;
- топоцентрический радиус-вектор спутника;
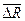 - вектор, соединяющий центр референц-эллипсоида и центр масс Земли.
- вектор, соединяющий центр референц-эллипсоида и центр масс Земли.
В некоторый момент UT-0=20h36m08.732s +№мин=20h38m08.732s c пункта P с известными координатами В=46˚58΄28,17˝, L=2h47m39.748s=41˚54΄56.22˝, Н=383,5м определены топоцентрические координаты спутника
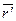 =812120+10м*№в;
=812120+10м*№в; 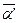 =18h46m57.275s+№в, сек; δ’=+38˚06΄52,24˝+№в, сек
=18h46m57.275s+№в, сек; δ’=+38˚06΄52,24˝+№в, сек
Необходимо найти геоцентрические координаты спутника. Предполагается, что синхронным методом определены углы Эйлера (ω=1,5˝, Ω=1,9˝, J=2,2˝). S0=16h47m01.535s, a=6378245м, α=2/298,3.
Табл.8
| исходные данные | ||||
| Cos | ||||
| UT | 8,73 | 0,9350171 | ||
| B | 28,17 | 0,682323894 | ||
| L | 56,22 | 0,744129493 | ||
| H | 383,5 | |||
| r | ||||
| a' | 52,28 | 0,946755022 | ||
| δ' | 47,24 | 0,786793684 | ||
| w | 1,5 | |||
| Ω | 1,9 | |||
| j | 2,2 | |||
| So | 1,53 | 0,957401384 | ||
| a | ||||
| N | 6389685,46 | |||
| v | 0,00273043 | |||
| ρ |
Порядок вычислений:
Табл.9
| 1. Вычисляем прямоугольные координаты пункта Р | |||
| X=(N+H)cosB∙cosL | 3244476,575 | ||
| Y=(N+H)cosB∙sinL | 2912698,978 | ||
| Z=[N(1-e2)+H]sinB | 4640189,221 | ||
| 2. Вычисляем координаты пункта Р в геоцентрической системе координат | |||
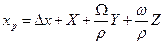
| 3244476,592 | ||
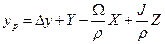
| 2912698,984 | ||
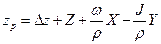
| 4640189,223 | ||
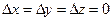
| |||
| S | 33,3 | ||
| cos | sin | ||
| (a-S) | 80,07893745 | 0,172291226 | 0,98504606 |
| 3. Находим прямоугольные координаты спутника, выполняя при этом переход от звездной системы координат к Гринвической. | |||
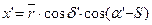
| 110102,633 | ||
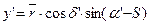
| 629493,255 | ||
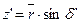
| 501315,251 | ||
| UT0=(S-S0)-(S-S0)v=20h36m08.732s | |||
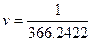
| |||
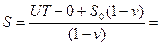 36h41m33.3343s 36h41m33.3343s
| |||
| 4. Находим сферические геоцентрические экваториальные координаты спутника. | |||
| xc = xp + x’ | 3354579,225 | ||
| yc = yp + y’ | 3542192,239 | ||
| zc = zp + z’ | 5141504,474 | ||
| 5. Находим сферические геоцентрические экваториальные координаты спутника | |||
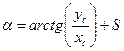
| 84h00m3.43s | ||
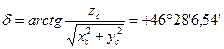
| 46˚30’12’’ | ||
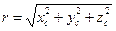
| 7087693,270 |
Фундаментальное уравнение космической геодезии
Дата добавления: 2015-06-10; просмотров: 3402;
