VIII. Вычисление топоцентрических экваториальных коордиант ИСЗ по результатам фотографических наблюдений.

При фотографировании ИСЗ на фоне звездного неба звезды изображаются в виде линий. За изображение ИСЗ принимается центр 3-го промежутка, для которого фиксируется время с точностью 1/1000 сек.

Общий порядок обработки фотографических наблюдений следующий:

Опознование опорных звезд на снимке с помощью звездного атласа
Выписка из каталога экваториальных координат звезд.
Вычисление поправок за прецессию, нутацию, абберацию и рефракцию.
измерение координат опорных звезд ИСЗ на негативе.
Вычисление топоцентрических коордиант ИСЗ.

Исходные координаты:

1)Момент наблюдения – август 03,77653^d,1998 UT-1

2) Фокусное расстояние камеры F=314.7 мм

3) Координаты пункта наблюдений

φ =38˚37΄57’’

λ =90˚29΄30’’

Н=67,3 м

4) Прямое восхождение оптической оси

А=14^h16^m30^s

5) Склонение оптической оси

D=40˚44΄31˝

6) Координаты звезд и спутника

Таблица 12

№ п/п	Координаты
экваториальные	прямоугольные
α_i (h)	δ_i (h)	x, мм	y, мм
	14,220230	41,02091	-5,7742	0,8134
	14,171309	38,57427	3,3665	9,0965
	14,124272	41,43019	1,4088	-6,478
	14,081726	40,58384	7,2095	-4,7697
	14,214995	39,31174	-2,3115	8,273
	14,171742	42,12020	-3,8993	-6,9351
ИСЗ			2,3426	3,6495

Порядок вычислений:

Вычисляем идеальные координаты на снимке ξ_i и η_i всех опорных звезд по формулам:

;

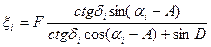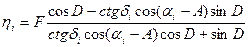где i=1,2,…,6.

Отдельно по абсциссам х и ординатам у составляем 2 системы уравнений поправок:

ax_i+by_i+c+l_xi=v_xi, где l_xi=x_i-ξ_i

dx_i+ey_i+f+l_yi=v_yi, где l_yi=y_i-η_i

где a, b,c,d,e,f – неизвестные пластинки.

Таблица 13

№п/п	Сtgδi	(αi-A)	cos (αi-A)	sin(αi-A)
	1,149521	-0,054770		-0,00096
	1,253833	-0,103691	0,999998	-0,00181
	1,133073	-0,150728	0,999997	-0,00263
	1,167386	-0,193274	0,999994	-0,00337
	1,221251	-0,060005	0,999999	-0,00105
	1,105938	-0,103258	0,999998	-0,00180

Выполняем решение систем уравнений по способу наименьших квадратов, для чего составляем отдельно по х и по у две системы по три нормальных уравнения в каждом.

[AA]a+[AB]b+[AC]c+[Al]_x=0

[AB]a+[BB]b+[BC]c+[Bl]_x=0

[AC]a+[BC]b+[CC]c+[Cl]_x=0

Из этой системы находим a, b, c

[AA]d+[AB]e+[AC]f+[Al]_y=0

[AB]d+[BB]e+[BC]f+[Bl]_y=0

[AC]d+[BC]e+[CC]f+[Cl]_y=0

Из этой системы находим d, e, f. Где:

Таблица 14

[AA]	Σх²	119,1839
[AB]	Σху	-9,66773
[AC}	Σх	-0,0002
[AL]x	Σxl_x	123,8299
[BB]	Σy²	264,6606
[BC]	Σy	1E-04
[BL]X	Σyl_x	-14,1046
[CC]	Σl
[CL]X	Σl_x	2,775199
[AL]Y	Σxl_y	51,5714
[BL]Y	Σyl_y	509,635
[CL]Y	Σl_y	7,672938

Полученные системы уравнений решаем по способу Гаусса

Табл.15

119,1839	-9,66773	-0,0002	123,79045
	0,081116	1,68E-06	-1,03865087
	264,6606	1E-04	-14,0574831
	263,8764	8,38E-05	-4,01608731
	-1	-3,2E-07	0,01521958
			2,81948909
			2,8196981
		-1	-0,46994968
-1,03865	0,01522	-0,46995
-7,9E-07	1,49E-07	С
0,001235	0,01522
-1,03742	b
119,1839	-9,66773	-0,0002	123,79045
а

Табл.16

119,1838883	-9,66772965	-0,0002	51,5714	Vx	Vy
	0,081116079	1,67808E-06	-0,4327	-0,01454845	-0,18402346
	264,6605949	1E-04	509,635	-0,011891643	0,015094129
	263,8763866	8,37768E-05	513,8183	-0,000496668	0,231029995
	-1	-3,17485E-07	-1,94719	-0,006085157	-0,164812503
			7,751012	-0,002467871	0,094371021
			7,750935	-0,00880023	0,008340818
		-1	-1,29182	0,000473879	0,123605945
-0,432704432	-1,947193014	-1,291823
-2,16778E-06	0,000000	f
-0,157948628	-1,947192603
-0,590655228	e
d

Полученные значения a, b, c, d, e, f подставляем в уравнение поправок, и вычисляем поправки v_xi и v_yi. После чего производим оценку точности.

Оценка точности:

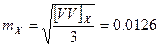
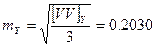
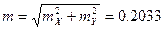
Используя полученные из решения нормальных уравнений постоянные пластинки a, b, c, d, e, f, вычисляем идеальные координаты спутника по формулам:

ζ_сп=ax_c_п + by_c_п + c_c_п + x_сп = -0,50206

η_сп=dy_c + cy_c + f_c + y_c = -6,13227

Вычисляем экваториальные сферические координаты спутника:

<4 5 678 9 10 >

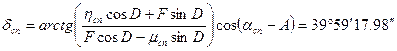
Дата добавления: 2015-06-10; просмотров: 2513;