VI. Определение пространственных геоцентрических инерциальных прямоугольных координат спутника.
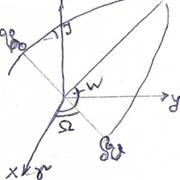
Табл.10
| исходные данные | |||||
| l1= | -0,01534129 | l2= | -0,9287415 | l3= | 0,370410516 |
| m1= | 0,75330076 | m2= | -0,2543368 | m3= | -0,60650699 |
| n1= | 0,65749723 | n2= | 0,26972592 | n3= | 0,7035235 |
| a= | 1,4 э.р | t= | 230,229167 | e= | 0,15 |
| T= | 41,025 | ||||
| μ= | r= | 1,193 |
Найти: X, Y, Z спутника
Решение:
- Определяем разность (t-T)m = 756,816666;
- Определяем эксцентрическую аномалию (Е):
Е=М + e∙sinE,
M=n∙(t-T)m = 40˚12’3,7’’
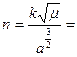0,053118386
Где k=0.07436574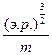 
;
E’=M+ e∙sinE = 40˚17’25,6’’
- Определяем прямоугольные координаты в плоскости орбиты:
xw =r∙cosV = 1,192051713
yw =r∙sinV = 0,047557483
rw = a(1-e∙cosE) = 1,039816985
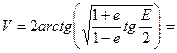37˚38΄42,09˝
- Определение пространственных прямоугольных координат:
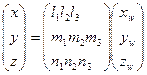
X = -0,711129374
Y = 0,833311393
Z = 0,9021488551
Контроль: R2 = x2+y2+z2 = x2w+y2w+z2w = r2w = 1,419.р.
Дата добавления: 2015-06-10; просмотров: 3780;