Z-преобразование

Иногда вместо преобразования Фурье используют Z-преобразование. Оно определяется формулой

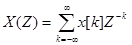(1)

В формуле (1) ряд является формальным, если же он сходится, то определяет аналитическую функцию. Для Z -преобразования справедливы аналоги свойств, доказанных для преобразования Фурье. Это же относится и к передаточной функции фильтра. В случае фильтра с бесконечным временем отклика

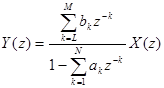(2)

Формула (2) удобна в том случае, когда переменная Z может принимать любые значения на комплексной плоскости. Еще раз обратим внимание на то, что в формуле (2) предполагается , что ряд для 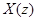имеет лишь конечное число ненулевых коэффициентов при положительных степенях. В этом случае мы можем в явной форме получить члены выходной последовательности.

Пример.

Пусть 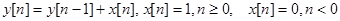. Будем предполагать, что 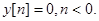Легко видеть, что решением является неограниченная последовательность 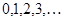. С другой стороны, согласно (2)

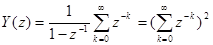
Формально возводя ряд в квадрат, получим тот же результат.

Условие устойчивости фильтра сводится к сходимости ряда для 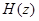при Z=1.