Z-преобразование (прямое и обратное, примеры). Основные теоремы Z-преобразования.

При большом числе разрядов АЦП цифровой сигнал x(n) эквивалентен дискретному сигналу 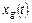, который представляется в виде последовательности взвешенных дельта-функций, площадь которых равна не единице, а значению непрерывного сигнала в моменты взятия отсчетов. Тогда, используя фильтрующее во времени свойство дельта-функций, запишем: где n - номера отсчетов.

Возьмем преобразование Лапласа от сигнала :

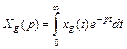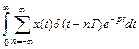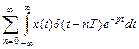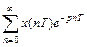= = = . (1)

По этому выражению определяется дискретное преобразование Лапласа (ДПЛ) по отсчетам x(nT) из непрерывного сигнала. Однако для описания цифровых систем ДПЛ не нашло широкого применения из-за неудобства, связанного с частым повторением в формулах ДПЛ функции 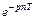. От этого недостатка свободно Z - преобразование, которое следует из ДПЛ введением новой комплексной переменной .

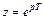Тогда из (1) имеем формулу прямого Z - преобразования для сигнала x(nT)

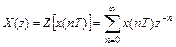. (2)

Сравнивая (1) и (2), видим, что формула для прямого Z - преобразования проще и компактнее формулы для прямого ДПЛ.

Примеры прямого Z - преобразования.

Единичный импульс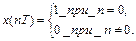

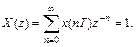
Аналогично для 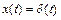имеем X(p)=1.

Единичный дискретный скачок

= .

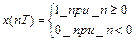
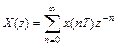Аналогично для x(t)=1(t) имеем откуда следует удобное для практики соответствие между переменной p в преобразовании Лапласа и переменной z в Z - преобразовании .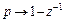

Наряду с прямым существует обратное Z - преобразование, которое определяется по выражению

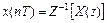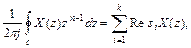= (3)

где 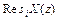- вычеты X(z). Однократные вычеты определяются по формуле

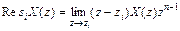(4)

Выражение для X(z) в этой формуле следует представлять в следующем виде:

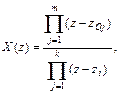
где 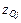, 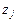- нули и полюсы функции X(z) соответственно. Часто букву Т в описании этих сигналов опускают, полагая Т=1, т.е. x(nT)=x(n).

Основные теоремы Z - преобразования

1) Линейность.

Если 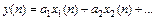, то .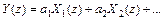

2) Смещение во времени.

Если 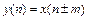, то .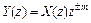

3) Разность дискретных функций.

Если 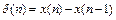, то = .

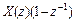Аналогия: если 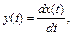то , .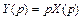

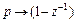4) Сумма дискретных функций.

Если 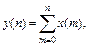то

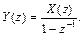
Аналогия: если 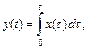то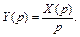

5) Свертка двух дискретных функций.

Если 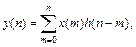то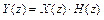

6) Предельные соотношения:

.

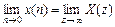
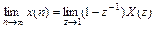
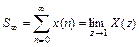Из этих теорем следует, что между преобразованием Лапласа и Z - преобразованием очень много общего.

34. Системная функция ЦСУ: определение, связь с разностным уравнением ЦСУ.

По аналогии с передаточными функциями для аналоговых систем в цифровых системах введено понятие системных функций, которые по определению есть отношение Z - преобразования от выходного цифрового сигнала y(nT) к Z - преобразованию от входного цифрового сигнала x(nT), т.е.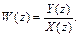

Дифференциальные уравнения применимы для аналоговых систем, а цифровые системы описываются разностными уравнениями. В разностных уравнениях время изменяется через конечный временной интервал Т, называемый периодом дискретизации.

Покажем на примере, как от дифференциального уравнения переходят к разностному уравнению.

Инерционное звено с передаточной функцией

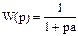
описывается дифференциальным уравнением, следующим из соотношения

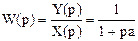, откуда Y(p) × (1+pa) = X(p), тогда

Так как ,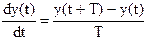

то введя в дифференциальное уравнение дискретное время nT вместо t, получим следующее разностное уравнение 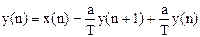, или

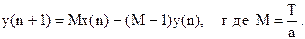
Этим уравнением описывается цифровое инерционное звено первого порядка.

Системные функции W(z) цифровых звеньев можно представить в двух формах:с положительными степенями z в виде

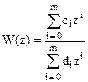, (1)

с отрицательными степенями z, которая получается из (1) умножением числителя и знаменателя на дробь 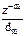тогда

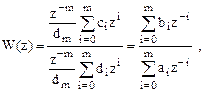(2)

где 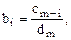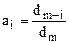, откуда а₀ = 1.

Вторая форма записи W(z) используется чаще.

По определению и с учетом (2) имеем:

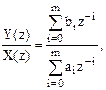
откуда .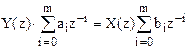

Перейдя от изображений к оригиналам, из этого выражения получим следующее разностное уравнение при а₀=1:

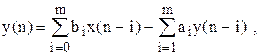(3)

где m - порядок разностного уравнения.

Таким образом из системной функции (2) однозначно определяется разностное уравнение (3) и наоборот, по разностному уравнению (3) однозначно определяется системная функция (2).