Признак и условие устойчивости замкнутых ЦСУ. ККП, АЧХ и ФЧХ цифровых САУ.

Признак устойчивости

Цифровая система считается устойчивой, если по окончании воздействия она с течением времени приходит в состояние покоя, т.е. 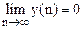. В противном случае система неустойчива.

Условие устойчивости

Цифровая система в общем случае описывается системной функцией 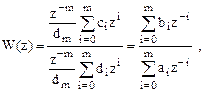(1)

или разностным уравнением 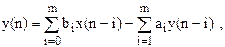. (2)

В системах без обратных связей коэффициенты a_i, 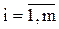в (1) и (2) равны нулю, такие системы всегда устойчивы.

В системах с обратными связями хотя бы один из коэффициентов a_i, , 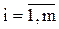не равен нулю. Такие системы могут быть неустойчивыми.

При прекращении входного воздействия x(n)=0, поэтому неоднородное разностное уравнение (2) превращается в однородное вида

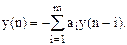
Решение этого уравнения имеет следующий вид

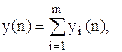где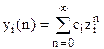

где c_i - коэффициенты, z_i - полюсы. Полюсы - это корни характеристического уравнения

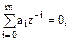
при которых системная функция (1) образуется в бесконечность. Характеристическое уравнение получается в результате приравнивания к нулю знаменателя системной функции (1).

Переход от ДПЛ к z- преобразованию по формуле замены z=e^pT преобразует левую полуплоскость p- плоскости в окружность единичного радиуса в Z плоскости. Графически это показано на рис.52.

Полюсы z_i в общем случае при действительных коэффициентах a_i в 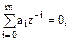являются комплексно-сопряженными, т.е.

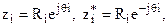
где R_i, q_i - полярные координаты полюсов z_i, z_i^* (см. рис.52).

Подставим эти значения в 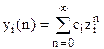и получим:

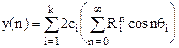
где 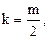если все полюса комплексно - сопряженные.

Из этого уравнения следует, что 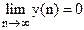при R_i<1. Таким образом цифровая система будет устойчива при условии, если полюсы ее системной функции находятся на Z- плоскости внутри окружности единичного радиуса.

На рис.52 полюсы z₁, z₁^* принадлежат устойчивой цифровой системе, а полюсы z₂, z₂^* принадлежат неустойчивой цифровой системе, т.к. у них R>1.

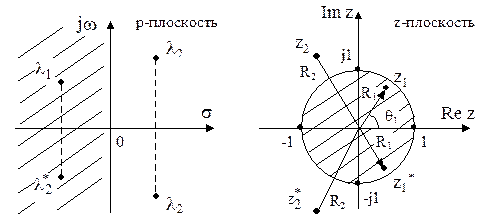
Рис.52 Графическая иллюстрация преобразования участков из комплексной p - плоскости в z - плоскость по формуле замены z=e^pT