Определение системных функций ЦСУ при различных схемах соединения звеньев. Прямая и каноническая схемы ЦСУ.

Также как и в аналоговых системах, для цифровых систем справедливы следующие соотношения:

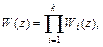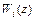при последовательном соединении цифровых звеньев результирующая системная функция где - системные функции звеньев,

при параллельном соединении цифровых звеньев

(

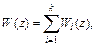при соединении звеньев по схеме с обратной связью, как на рис.36а

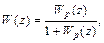
при соединении звеньев по схеме с обратной связью, как на рис.36б

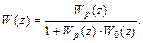
В теории дробно-рациональных функций доказано, что системная функция при четных m может быть представлена

= , = ,

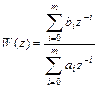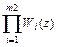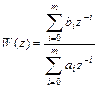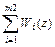где 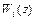- системные функции биквадратных звеньев, которые описываются выражением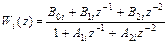

При параллель­ном соединении соответствует следующее разностное уравнение (индекс опущен)

+ - .

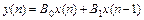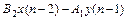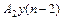Вычисление этого разностного уравнения осуществляется по схеме цифрового звена, приведенной на рис.51а. Первая часть называется нерекурсивной, а вторая часть схемы с обратными связями называется рекурсивной. Нерекурсивной части соответствует числитель выражения 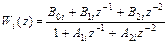, а рекурсивной части соответствует знаменатель этого выражения. Блоки реализуют цифровую линию задержки- последовательный регистр.

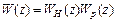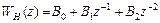где - системная функция нерекурсивной части схемы,

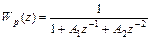- системная функция рекурсивной части схемы.

Так как от перестановки сомножителей произведения не меняется, то выраже­ние 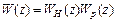можно представить в виде .

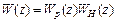Этому выражению соответствует схема цифрового звена второго порядка, при­веденная на рис.516.

Так как в этом случае линии задержки рекурсивной и нерекурсивной частей схемы идут параллельно, то их объединяют в одну. Схема на рис.516 получила название канонической (образцовой), так как в ней число элементов задержки в 2 раза меньше, чем в схеме на рис.51а.

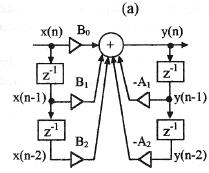
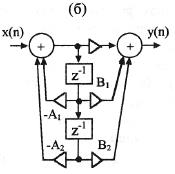
Рис.51 Эквивалентные схемы цифрового биквадратного звена: прямая (а) и каноническая (б)