Связь между передаточными и системными функциями при использовании стандартного и билинейного Z-преобразования.

Также, как от дифференциальных уравнений можно перейти к разностным уравнениям, от передаточных функций аналоговых систем W(p) можно перейти к системным функциям W(z). Этот переход можно сделать двумя способами:

с помощью стандартного Z - преобразования,

с помощью билинейного Z - преобразования.

При использовании стандартного Z - преобразования переход от W(p) к W(z) осуществляется заменой 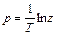, т.е.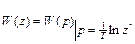

Обратный переход делается по правилу

.

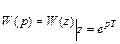Указанные переходы следуют из прямого 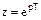и обратного 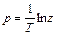выражений, связывающих ДПЛ и Z - преобразования.

Переход от W(p) к W(z) с помощью стандартного Z - преобразования обеспечивает высокую точность, но в результате вместо дробно-рациональных функций получаются выражения с трансцендентыми функциями, что очень неудобно для выполнения различных математических операций над ними.

От указанного недостатка свободен переход от W(p) к W(z) и обратно с помощью билинейного Z - преобразования. Это преобразование приближенное, но при этом сохраняются дробно-рациональные функции в выражениях W(p) и W(z).

При билинейном Z - преобразовании используется разложение в степенной ряд функции

.

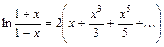Ограничившись первым членом ряда, получим .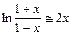

Обозначим 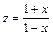, откуда .

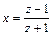Тогда 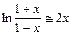перепишем в виде .

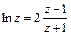Т.к. 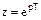, то ln z = pT. Приравняем правые части и получим приближенную линейную связь между p и z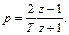

Из 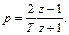следует обратная связь между z и p .

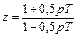Тогда переход от W(p) к W(z) с помощью билинейного Z- преобразования осуществляется по формуле .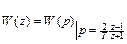

Обратный переход от W(z) до W(p) осуществляется по формуле .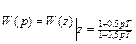

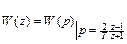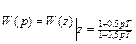В результате переходов от W(p) к W(z) и обратно по и сохраняется дробно-рациональный вид функций, причем степень функций не изменяется.