А квадрат середньоквадратичної похибки окремого вимірювання – дисперсії
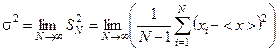 . (1.11)
. (1.11)
На практиці необхідно знати ймовірність того, що абсолютна величина похибки вимірювань не перевищує деякого заздалегідь заданого значення, наприклад 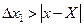 . Цю ймовірність можна визначити за кривою Гауса (рис. 1.3). Проведемо ординати, які відповідають значенням
. Цю ймовірність можна визначити за кривою Гауса (рис. 1.3). Проведемо ординати, які відповідають значенням 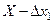 та
та 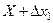 (рис. 1.3). Заштрихована частина площини, яка міститься між вказаними ординатами, віссю абсцис і кривою Гауса, чисельно дорівнюватиме ймовірності того, що абсолютна величина похибки вимірювань не перевищує значення
(рис. 1.3). Заштрихована частина площини, яка міститься між вказаними ординатами, віссю абсцис і кривою Гауса, чисельно дорівнюватиме ймовірності того, що абсолютна величина похибки вимірювань не перевищує значення 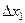 . Зі зменшенням
. Зі зменшенням 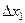 зменшується і заштрихована площина, тобто зменшується ймовірність появи похибки за модулем від 0 до
зменшується і заштрихована площина, тобто зменшується ймовірність появи похибки за модулем від 0 до 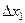 . У табл. 1.1 наведено цю ймовірність для деяких значень похибки
. У табл. 1.1 наведено цю ймовірність для деяких значень похибки 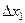 . Значення похибки взято в масштабі
. Значення похибки взято в масштабі 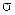 , що зручно для порівняння ймовірностей різних похибок.
, що зручно для порівняння ймовірностей різних похибок.
Таблиця 1.1
Значення похибки 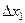
| 1 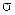
| 2 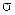
| 3 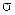
|
Імовірність 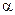 того, що результат вимірювання того, що результат вимірювання 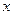 належить інтервалу належить інтервалу 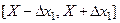
| 0,683 | 0,954 | 0,997 |
З табл. 1.1 випливає, що коли ми виконаємо 1000 дослідів, то приблизно у 683 дослідах абсолютна похибка буде меншою або дорівнювати 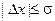 . Можна стверджувати, із імовірністю0,683 результат вимірювання
. Можна стверджувати, із імовірністю0,683 результат вимірювання 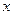 належатиме інтервалу
належатиме інтервалу 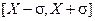 або
або
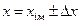 , (1.12)
, (1.12)
де 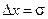 ,
, 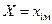 . Знайдену таким чином похибку (
. Знайдену таким чином похибку ( 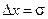 ) називають стандартним відхиленням, або стандартною похибкою.
) називають стандартним відхиленням, або стандартною похибкою.
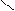
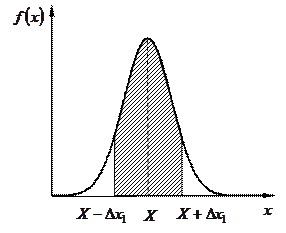

Рисунок 1.3
Якщо вибрати іншу ширину інтервалу, тоді звичайно ймовірність буде теж іншою. Наприклад, виберемо 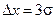 . Тоді результат вимірювання належатиме інтервалу (1.12) вже з імовірністю 0,997. Такий алгоритм розрахунку випадкової похибки називають правилом “трьох сигм”.
. Тоді результат вимірювання належатиме інтервалу (1.12) вже з імовірністю 0,997. Такий алгоритм розрахунку випадкової похибки називають правилом “трьох сигм”.
Як бачимо, випадкову похибку необхідно характеризувати як модулем самої похибки, так і відповідною ймовірністю. Інтервал 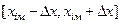 називають довірчим інтервалом, а ймовірність потрапляння значення виміряної величини в цей інтервал – довірчою ймовірністю.
називають довірчим інтервалом, а ймовірність потрапляння значення виміряної величини в цей інтервал – довірчою ймовірністю.
Таким чином, для характеристики випадкової похибки необхідно задавати довірчий інтервал і довірчу ймовірність. Абсолютна похибка, що визначає подвійну ширину довірчого інтервалу, може бути поданою у вигляді
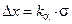 , (1.13)
, (1.13)
де 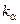 – деякий коефіцієнт, що залежить від довірчої ймовірності
– деякий коефіцієнт, що залежить від довірчої ймовірності 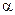 .
.
Дата добавления: 2015-05-05; просмотров: 1380;
