Деякі положення теорії ймовірностей

Щоб відповісти на вищесформовані питання, розглянемо деякі положення теорії ймовірності.

Під імовірністю випадкової події розуміють границю відношення кількості випадків 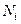, коли ця подія відбувається, до загальної кількості вимірювань 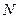, за умови, що кількість вимірювань прямує до нескінченності:

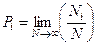. (1.5)

Розглянемо закономірності, яким підлягає ймовірність появи виміряних значень 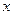фізичної величини. Для цього запишемо виміряні значення фізичної величини 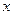у порядку їх зростання. Розіб'ємо весь діапазон виміряних значень на інтервали 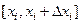. Порахуємо, скільки разів 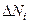виміряна величина потрапляє в i-й інтервал 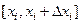. Потім побудуємо діаграму, яка показує, як часто з'являлися під час вимірювань ті чи інші значення 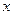. Будемо відкладати на осі абсцис значення вибраних інтервалів, а на осі ординат – кількість вимірювань 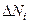, які потрапляють у даний інтервал. Така діаграма (рис. 1.1) називається гістограмою.

Аналізуючи рис. 1.1, можна дійти висновку, що деякі значення виміряної величини 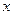з'являються частіше, ніж інші, тобто ймовірність появи різних значень 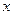є неоднаковою.

Зрозуміло, що коли загальна кількість вимірювань 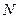прямуватиме до нескінченності ( 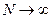), то кількість вимірювань 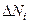, які потрапляють у i-й інтервал 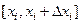, також будуть прямувати до нескінченності ( 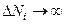). Тому більш зручно відкладати вздовж осі ординат не величину 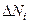, а відношення 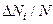, яке у випадку, коли 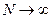дорівнює імовірності 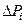того, що значення величини 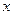під час вимірювання потрапляють у інтервал .

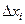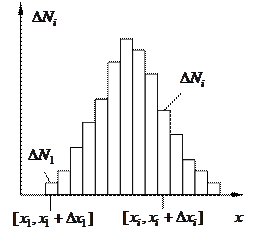
Рисунок 1.1

З іншого боку, зрозуміло, що чим більшою буде ширина інтервалу 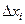, тим більшою буде ймовірність 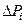того, чи буде виміряна величина перебувати у цьому інтервалі 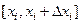. Використовуючи цю властивість, для характеристики розподілу ймовірностей величини 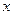вводять функцію розподілу ймовірностей, яка визначається співвідношенням

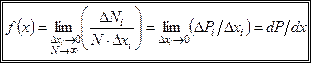. (1.6)

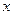Функція розподілу ймовірностей характеризує, як змінюється ймовірність залежно від вимірюваної величини . Зрозуміло, що вигляд цієї функції буде подібним до рис. 1.1, у якому через зменшення ширини інтервалів до нуля гістограма перетворюється у криву. Типова крива розподілу ймовірностей виміряних значень подана на рис. 1.2.

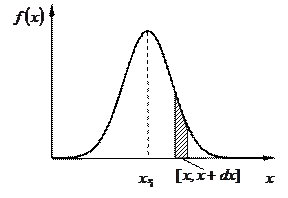
Рисунок 1.2

Із визначення (1.6) випливає, що добуток 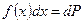визначає ймовірність того, що значення вимірюваної величини належатиме інтервалу 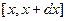. Ця ймовірність чисельно дорівнює площі заштрихованої на рис. 1.2 фігури. Таким чином, визначаючи відповідну площу під кривою розподілу 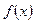, знаходимо ймовірність появи вимірюваної величини в інтервалі від 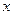до .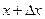

Як випливає з рис. 1.2, крива розподілу 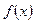має чіткий максимум при 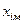. Це означає, що при великій кількості вимірювань поява значень, які відповідають величині 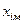, має найбільшу ймовірність. Тому 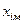, яка відповідає максимальному значенню функції розподілу 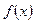, називають найбільш імовірним значенням вимірюваної величини 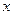. Також із рис. 1.2 випливає, що крива розподілу густини ймовірностей симетрична відносно найбільш імовірного значення 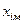вимірюваної величини.

Звідси випливає, що за справжнє значення 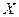вимірюваної величини потрібно брати найбільш імовірне значення .

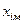Проводячи експериментальні дослідження різних величин, які мають випадкові похибки, ми будемо отримувати криві функцій розподілу 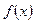, вигляд яких подібний до кривої, що зображена на рис. 1.2. Виникає питання, яким буде аналітичний вигляд таких кривих? Відповідь на це питання вперше була отримана французьким математиком Муавром у 1733 році. Потім знайдена функція була детально вивчена німецьким математиком Гаусом і отримала назву функції розподілу Гауса. Функція розподілу Гауса має вигляд

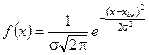, (1.7)

де 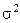– стала величина, яка називається дисперсією.

Закон розподілу Гауса (1.7) часто називають законом нормального розподілу. Цим, з одного боку, підкреслюють його універсальність, а з іншого – припускають можливість існування й інших законів розподілу, які відрізняються від нормального.

Таким чином, функція розподілу величин, що мають випадкові похибки, визначається розподілом Гауса (1.7), який, у свою чергу, залежить лише від двох параметрів: 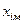– найбільш імовірного значення вимірюваної величини та 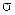– дисперсії розподілу. Це означає, що для опису розподілу фізичної величини, яка має випадкові похибки, достатньо визначити найбільш імовірне значення 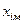та дисперсію .

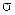Перш ніж подати формули, які дозволяють знайти 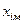та 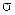, дамо декілька визначень. Середнім арифметичним значенням називають величину

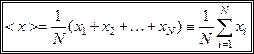, (1.8)

де 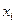– значення досліджуваної величини; 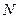– загальна кількість вимірювань. Зазначимо, середнє арифметичне значення часто позначається так: , , .

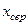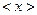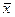Середньоквадратичною похибкою окремого вимірювання називається величина

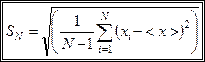. (1.9)

Як з’ясовано у теорії ймовірностей, при нескінченно великій кількості вимірювань середнє арифметичне дорівнює найбільш імовірному значенню, а отже, і справжньому значенню виміряної величини:

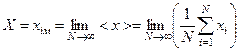, (1.10)