Головні положення розрахунків металевих конструкцій на монтажні навантаження та становища.

2.1. Для засвоєння теми необхідні знання методик розрахунків металевих конструкцій по допустимих та граничних станах; типи напруг в монтажних блоках: основні, додаткові, місцеві й початкові, різниця в принципах підходу до методик розрахунку по граничних станах і по допустимих напругах.

2.2. Монтажні навантаження та впливи, класифікація й визначення:

■ постійні;

■ тимчасові;

■ вітрові

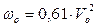(Па), (2.1)

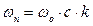(Па), (2.2)

й далі необхідно знати методику визначення k та c. При цьому “c” може бути визначено для окремих елементів з прокату й труб, плоских ферм:

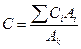
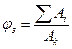- коефіцієнт заповнення.

Поняття про число Рейнольдса. Просторові блоки, ряд плоских ферм, споруди з циліндричною поверхнею (передбачається знання СниП 2.01.07 – 85*);

- від ваги монтажних механізмів та обладнання, зокрема, один з самих складних випадків – зусилля від розчалок (див. [1]):

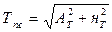, (2.3)

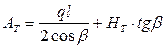, (2.4)

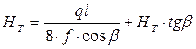, (2.5)

В формулах (2.3), (2.4) й (2.5) А_т і Н_т верикальна та горизонтальна складова від сили тяжіння розчалки Т;

β – кут між лінією, що з’єднує точки А та Б й горизонтом,

- інерційні навантаження та впливи;

- динамічні впливи частин, що звішуються;

- навантаження від можливих ударів:

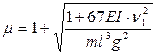, (2.6)

- навантаження від тиску рідини, газів та інших матеріалів для випробування.

Закон Бойля-Маріотта:

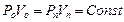, (2.7)

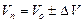, (2.7а)

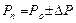, (2.7б)

отже

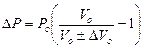, (2.7в)

Закон Клапейрона:

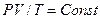(2.8)

- температурні навантаження та впливи:

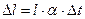(2.9)

- елементарний випадок.

Загальний випадок:

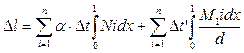(2.10)

- переміщення опор або інших в’язів.

2.3. Визначення зусиль і деформацій в елементах металевих конструкцій від монтажних навантажень та впливів:

- при загальних схемах балок та колон за звичайними правилами будівельної механіки;

- якщо ферма розглядається як пружна пластина, то власна вага вважається прикладеною на висоті від верха:

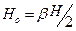, (2.11)

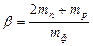, (2.12)

- вибір розрахункової схеми та основної системи виконуються за правилами будівельної механіки;

- врахування супутніх впливів;

- особливості розрахунку статично невизначених систем (згідно з правилами будівельної механіки).

2.4. Приклад визначення горизонтального переміщення точки Д та кутового переміщення січення С для стержня, що наведено на рис. 2.1.

1 випадок: температура підвищується равномірно в ригелі та лівій стійці на ∆t. В цьому разі ∆t = 0. Отже, другої складової частини в формулі (2.10) не буде. Потрібно побудувати тільки одиничні епюри М та N від сили X_l = 1 в точці Д (рис.2.2)

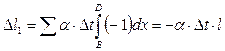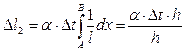; (рис.2.3)